MATH 427: Intro to Machine Learning

Eric Friedlander

Pre-Survey

Take 10 minute and fill our this survey.

If you chose to opt-out please read as much of this article as you an in 8 minutes and then fill out this survey.

Data Generating Process

Suppose we have

  • Features: \(\mathbf{X}\)
  • Target: \(Y\)
  • Goal: Predict \(Y\) using \(\mathbf{X}\)
  • Data generating process: underlying, unseen and unknowable process that generates \(Y\) given \(\mathbf{X}\)

Population

More mathematically, the “true”/population model can be represented by

\[Y=f(\mathbf{X}) + \epsilon\]

where \(\epsilon\) is a random error term (includes measurement error, other discrepancies) independent of \(\mathbf{X}\) and has mean zero.

GOAL: Estimate \(f\)

Why Estimate \(f(\mathbf{X})\)?

We wish to know about \(f(\mathbf{X})\) for two reasons:

  1. Prediction: make an educated guess for what \(y\) should be given a new \(x_0\): \[\hat{y}_0=\hat{f}(x_0) \ \ \ \text{or} \ \ \ \hat{y}_0=\hat{C}(x_0)\]
  2. Inference: Understand the relationship between \(\mathbf{X}\) and \(Y\).
  • An ML algorithm that is developed mainly for predictive purposes is often termed as a Black Box algorithm.

Prediction

There are two types of prediction problems:

  • Regression (response \(Y\) is quantitative): Build a model \(\hat{Y} = \hat{f}(\mathbf{X})\)
  • Classification (response \(Y\) is qualitative/categorical): Build a classifier \(\hat{Y}=\hat{C}(\mathbf{X})\)
  • Note: a “hat”, \(\hat{\phantom{f}}\), over an object represents an estimate of that object
    • E.g. \(\hat{Y}\) is an estimate of \(Y\) and \(\hat{f}\) is an estimate of \(f\)

Prediction and Inference

Income dataset

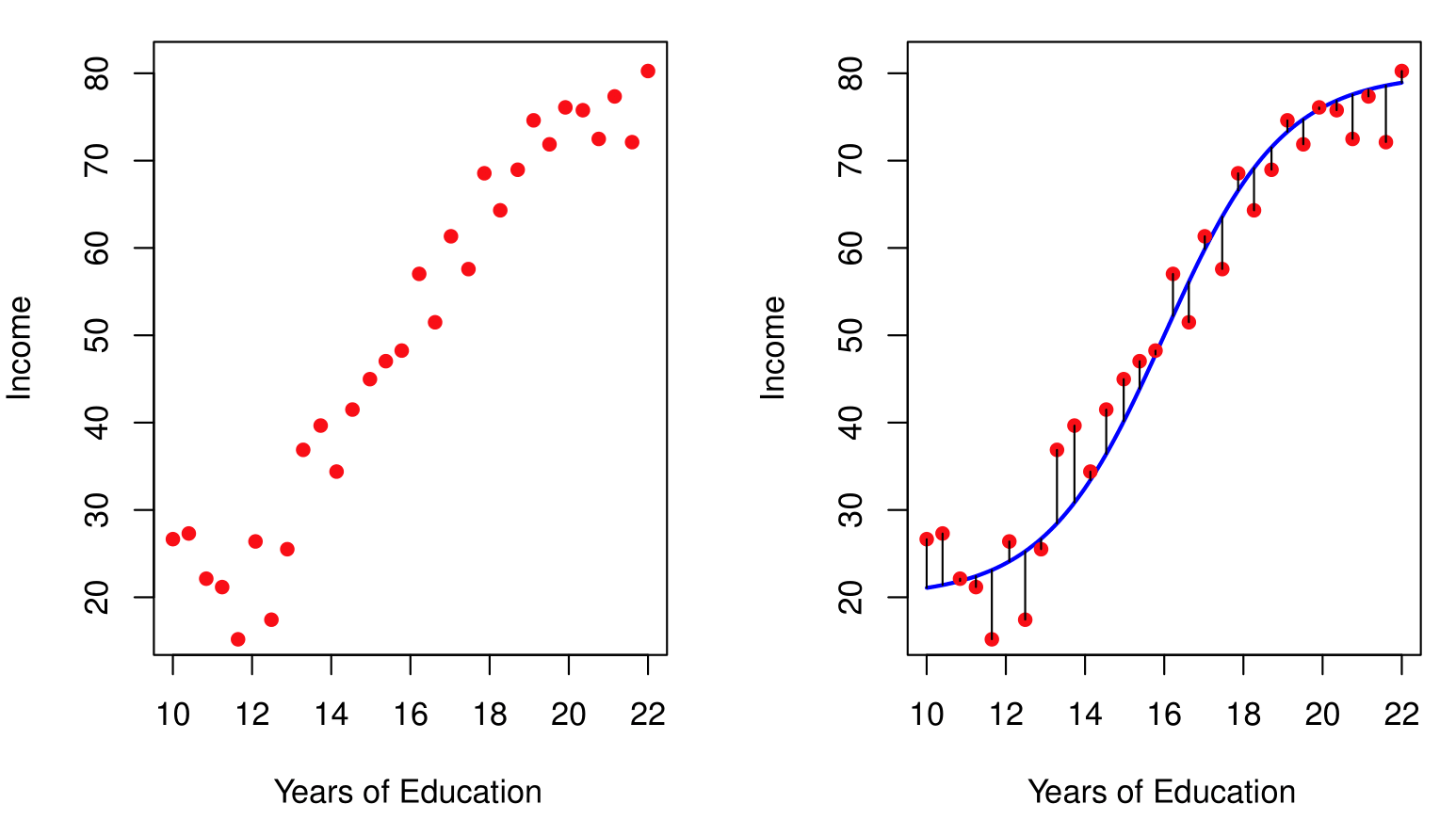
Why ML? (from ISLR2)

Prediction and Inference

Income dataset

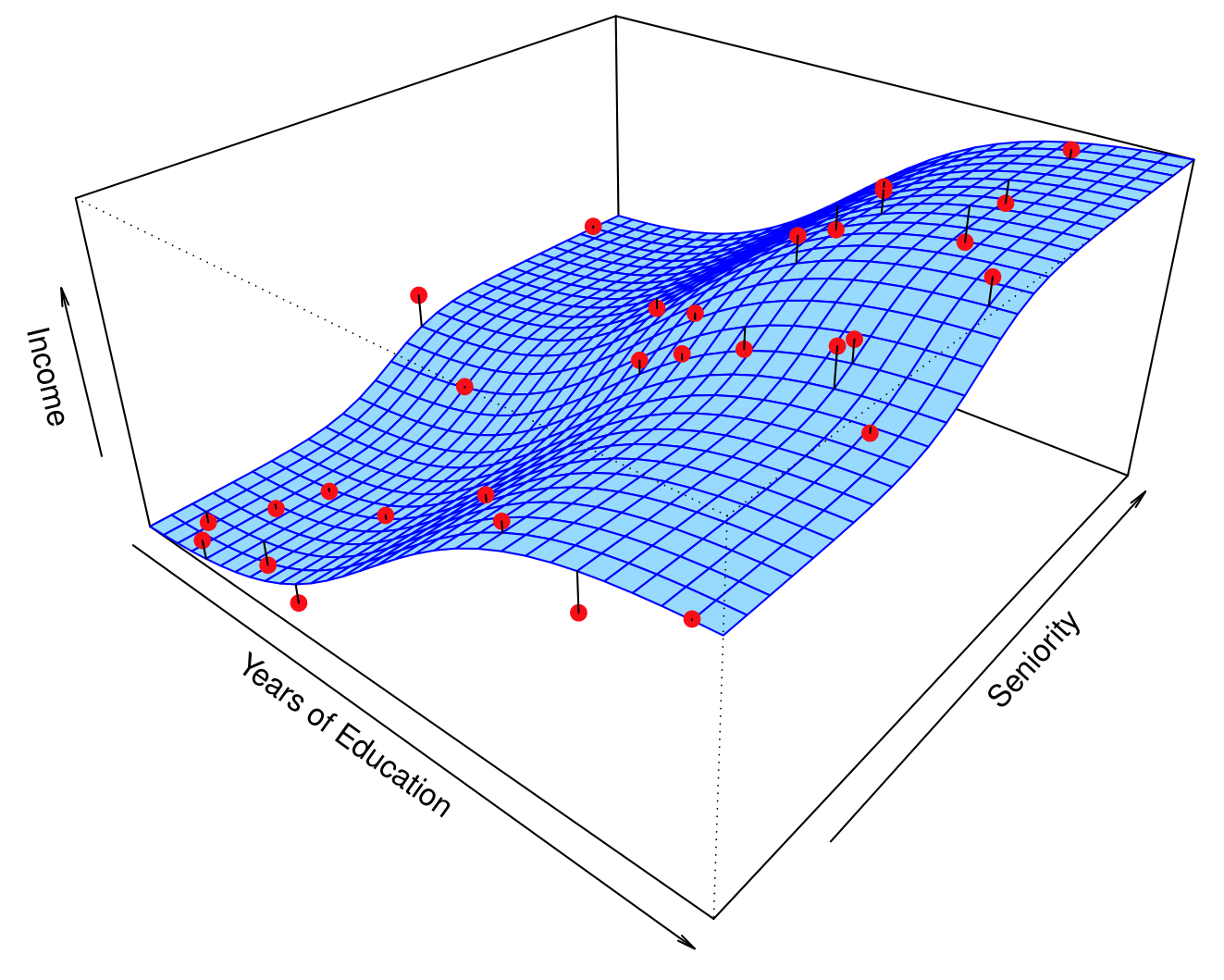
Why ML? (from ISLR2)

Question!!!

Based on the previous two slides, which of the following statements are correct?

  1. As Years of Education increases, Income increases, keeping Seniority fixed.
  2. As Years of Education increases, Income decreases, keeping Seniority fixed.
  3. As Years of Education increases, Income increases.
  4. As Seniority increases, Income increases, keeping Years of Education fixed.
  5. As Seniority increases, Income decreases, keeping Years of Education fixed.
  6. As Seniority increases, Income increases.
  1. As Years of Education increases, Income increases, keeping Seniority fixed. TRUE
  2. As Years of Education increases, Income decreases, keeping Seniority fixed. FALSE
  3. As Years of Education increases, Income increases. TRUE
  4. As Seniority increases, Income increases, keeping Years of Education fixed. TRUE
  5. As Seniority increases, Income decreases, keeping Years of Education fixed. FALSE
  6. As Seniority increases, Income increases. TRUE

Discussion

What’s the difference between these two statements:

  1. As Years of Education increases, Income increases, keeping Seniority fixed.
  2. As Years of Education increases, Income increases.

How Do We Estimate \(f(\mathbf{X})\)?

Broadly speaking, we have two approaches.

  1. Parametric methods
  2. Non-parametric methods

Parametric Methods

  • Assume a functional form for \(f(\mathbf{X})\)
    • Linear Regression: \(f(\mathbf{X})=\beta_0 + \beta_1 \mathbf{x}_1 + \beta_2 \mathbf{x}_2 + \ldots + \beta_p \mathbf{x}_p\)
    • Estimate the parameters \(\beta_0, \beta_1, \ldots, \beta_p\) using labeled data
  • Choosing \(\beta\)’s that minimize some error metrics is called fitting the model
  • The data we use to fit the model is called our training data

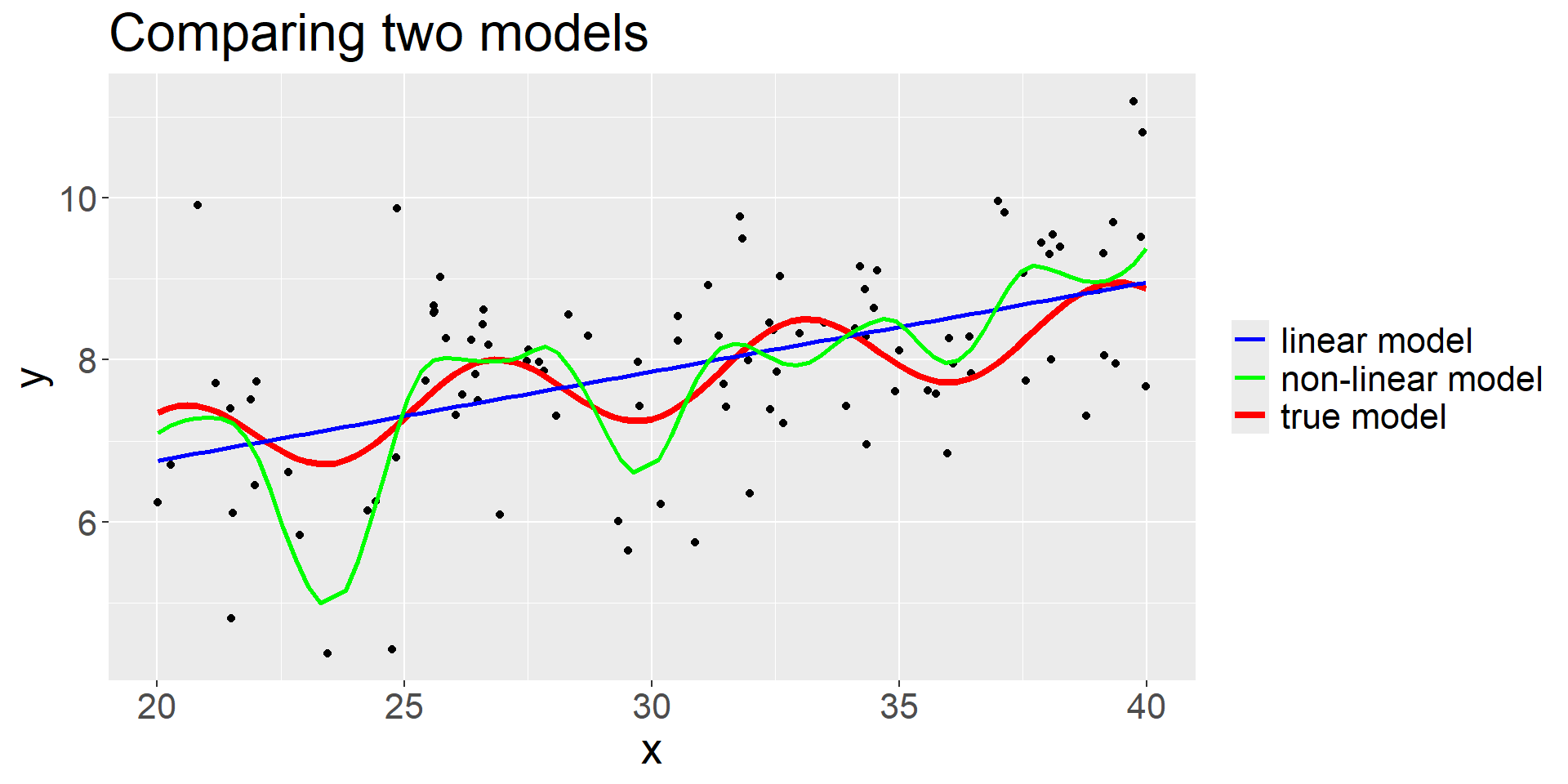
Parametric Methods

Parametric model fit (from ISLR2)

  • What are some potential parametric models that could result in this picture?
  • Note: Right line is the true relationship

Parametric Methods

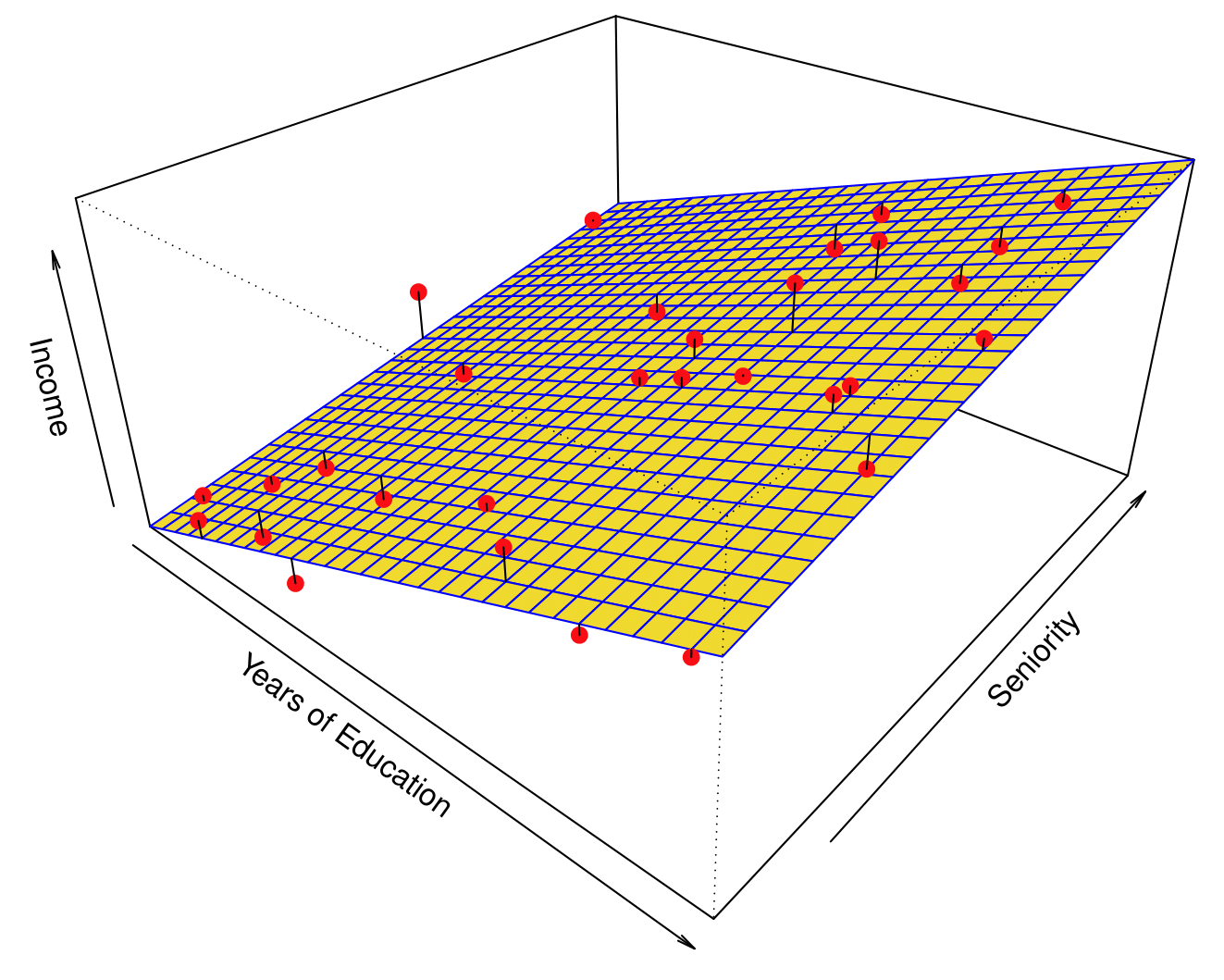
Income dataset

True relationship

Parametric model

From ISLR2

  • What are some functions that could have resulted in the model on the right?
  • \(\text{Income} \approx \beta_0 + \beta_1\times\text{Years of Education} + \beta_2\times\text{Seniority}\)

Non-parametric Methods

  • Non-parametric approach: no explicit assumptions about the functional form of \(f(\mathbf{X})\)
  • Much more observations (compared to a parametric approach) required to fit non-parametric model
    • Idea: parametric model restricts space of possible answers

Income dataset

True relationship

Non-parametric model fit

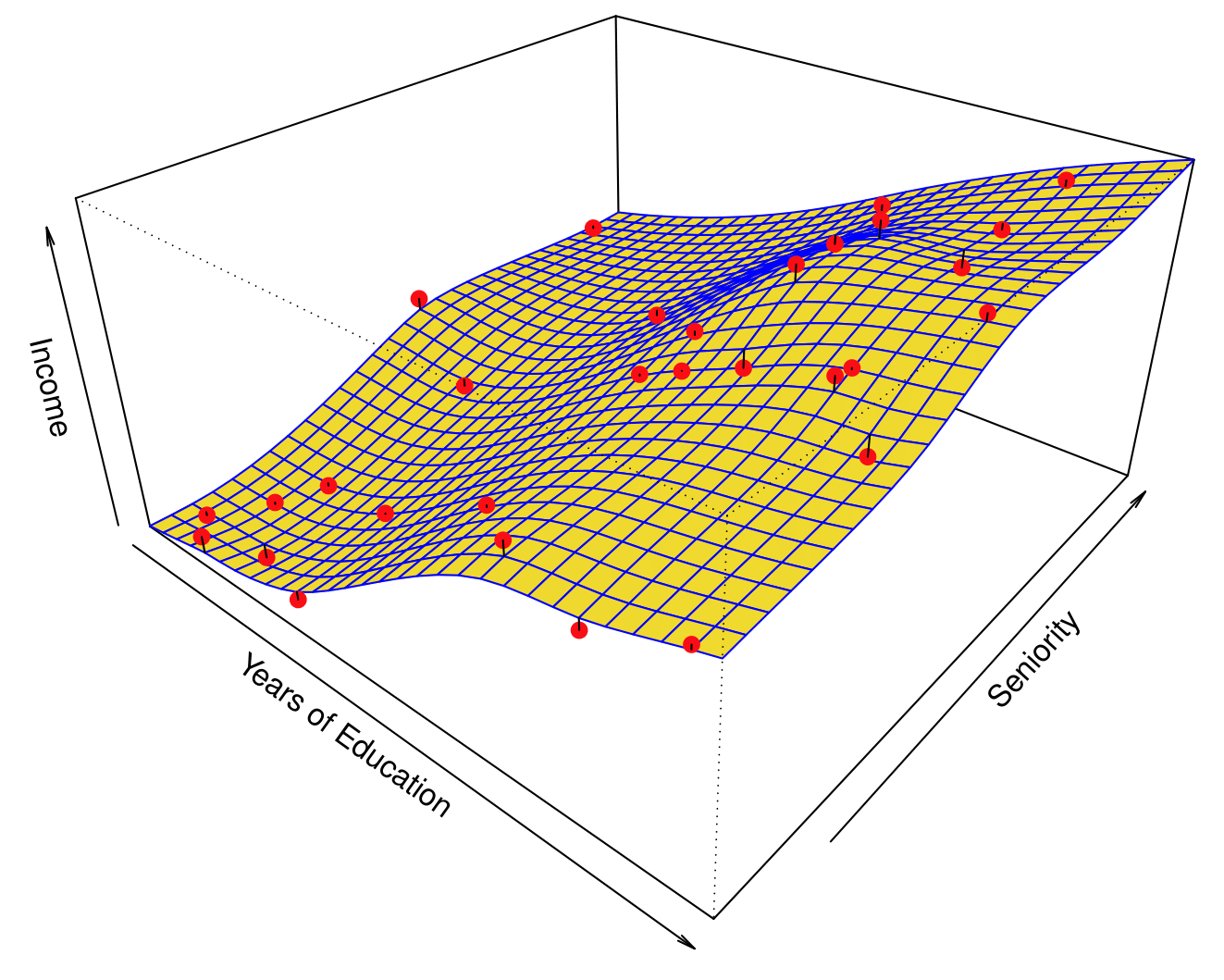
From ISLR2

Supervised Learning: Flexibility of Models

  • Flexibility: smoothness of functions
  • More theoretically: how many parameters are there to estimate?

[More flexible \(\implies\) More complex \(\implies\) Less Smooth \(\implies\) Less Restrictive \(\implies\) Less Interpretable

Supervised Learning: Some Trade-offs

  • Prediction Accuracy versus Interpretability
  • Good Fit versus Over-fit or Under-fit

Trade-off between flexibility and interpretability (from ISLR2)

Supervised Learning: Selecting a Model

  • Why so many different ML techniques?
  • There is no free lunch in statistics: All methods have different pros and cons
    • Must select correct model for each use-case
  • Relevant questions in model selection:
    • How much observations \(n\) and variables \(p\)?
    • What is the relative importance is prediction, interpretability, and inference?
    • Do we expect relationship to be non-linear?
    • Regression or classification?

Supervised Learning: Assessing Model Performance

  • When we estimate \(f(\mathbf{X})\) using \(\hat{f}(\mathbf{X})\), then,

\[\underbrace{E\left[Y-\hat{Y}\right]^2}_{Error}=E\left[f(\mathbf{X})+\epsilon - \hat{f}(\mathbf{X})\right]^2=\underbrace{E\left[f(\mathbf{X})-\hat{f}(\mathbf{X})\right]^2}_{Reducible} + \underbrace{Var(\epsilon)}_{Irreducible}\]

  • \(E\left[Y-\hat{Y}\right]^2\): Expected (average) squared difference between predicted and actual (observed) response, Mean Squared Error (MSE)
  • Goal: find an estimate of \(f(\mathbf{X})\) to minimize the reducible error

Supervised Learning: Assessing Model Performance

  • Labeled training data \((x_1,y_1), (x_2, y_2), \ldots, (x_n,y_n)\)
    • i.e. \(n\) training observations
  • Fit/train a model from training data
    • \(\hat{y}=\hat{f}(x)\), regression
    • \(\hat{y}=\hat{C}(x)\), classification
  • Obtain estimates \(\hat{f}(x_1), \hat{f}(x_2), \ldots, \hat{f}(x_n)\) (or, \(\hat{C}(x_1), \hat{C}(x_2), \ldots, \hat{C}(x_n)\)) of training data
  • Compute error:
    • Regression \[\text{Training MSE}=\text{Average}_{Training} \left(y-\hat{f}(x)\right)^2 = \frac{1}{n} \displaystyle \sum_{i=1}^{n} \left(y_i-\hat{f}(x_i)\right)^2\]
    • Classification \[ \begin{aligned} \text{Training Error Rate} &=\text{Average}_{Training} \ \left[I \left(y\ne\hat{C}(x)\right) \right]\\ &= \frac{1}{n} \displaystyle \sum_{i=1}^{n} \ I\left(y_i \ne \hat{C}(x_i)\right) \end{aligned} \]

Recap

  • Regression vs. Classification
  • Parametric vs. non-parametric models
  • Training v. test data
  • Assessing regression models: Mean-Squared Error
  • Trade-offs:
    • Flexibility vs. interpretability
    • Bias vs. variance

🔗 MAT 427 - Spring 2025 - Schedule