MATH 427: Simple Linear Regression + Gradient Descent

Eric Friedlander

Concept Check

What do we call these:

$\mathbf{X}$
$Y$

What is our goal in supervised learning?

Concept Check

Features: $\mathbf{X}$
Target: $Y$
Goal: Predict $Y$ using $\mathbf{X}$

What do we call this process if $Y$ is numerical? What about categorical?

Concept Check

What do we call this process if $Y$ is numerical? What about categorical?
- Numerical: regression
- Categorical: classification

What is the difference between a training and a test set?
How do we evaluate the performance of a regression model?

Bias-Variance Trade-Off

Supervised Learning: Assessing Model Performance

Labeled training data $(x_1,y_1), (x_2, y_2), \ldots, (x_n,y_n)$
- i.e. $n$ training observations
Fit/train a model from training data
- $\hat{y}=\hat{f}(x)$, regression
- $\hat{y}=\hat{C}(x)$, classification
Obtain estimates $\hat{f}(x_1), \hat{f}(x_2), \ldots, \hat{f}(x_n)$ (or, $\hat{C}(x_1), \hat{C}(x_2), \ldots, \hat{C}(x_n)$) of training data
Compute error:
- Regression \[\text{Training MSE}=\text{Average}_{Training} \left(y-\hat{f}(x)\right)^2 = \frac{1}{n} \displaystyle \sum_{i=1}^{n} \left(y_i-\hat{f}(x_i)\right)^2\]
- Classification \[ \begin{aligned} \text{Training Error Rate} &=\text{Average}_{Training} \ \left[I \left(y\ne\hat{C}(x)\right) \right]\\ &= \frac{1}{n} \displaystyle \sum_{i=1}^{n} \ I\left(y_i \ne \hat{C}(x_i)\right) \end{aligned} \]

Supervised Learning: Assessing Model Performance

In general, not interested in performance on training data
Want: performance on unseen test data… why?
Fresh test data: $(x_1^{test},y_1^{test}), (x_2^{test},y_2^{test}), \ldots, (x_m^{test},y_m^{test})$.
Compute test error:
- Regression \[\text{Test MSE}=\text{Average}_{Test} \left(y-\hat{f}(x)\right)^2 = \frac{1}{m} \displaystyle \sum_{i=1}^{m} \left(y_i^{test}-\hat{f}(x_i^{test})\right)^2\]
- Classification \[\text{Test Error Rate}=\text{Average}_{Test} \ \left[I \left(y\ne\hat{C}(x)\right) \right]= \frac{1}{m} \displaystyle \sum_{i=1}^{m} \ I\left(y_i^{test} \ne \hat{C}(x_i^{test})\right)\]

Supervised Learning: Bias-Variance Trade-off

Model fit on training data $\hat{f}(x)$
“True” relationship: $Y=f(x)+\epsilon$
$(x_0^{test}, y_0^{test})$: test observation
Bias-Variance Trade-Off (Theoretical) \[\underbrace{E\left(y_0^{test}-\hat{f}(x_0^{test})\right)^2}_{total \ error}=\underbrace{Var\left(\hat{f}(x_0^{test})\right)}_{source \ 1} + \underbrace{\left[Bias\left(\hat{f}(x_0^{test})\right)\right]^2}_{source \ 2}+\underbrace{Var(\epsilon)}_{source \ 3}\] where $Bias\left(\hat{f}(x_0)\right)=E\left(\hat{f}(x_0)\right)-f(x_0)$

Question: Where is $\hat{y}_0^{test}$?

Supervised Learning: Bias-Variance Trade-off

Reducible Error:
- Source 1: how $\hat{f}(x)$ varies among different randomly selected possible training data (Variance)
- Source 2: how $\hat{f}(x)$ (when predicting the test data) differs from its target $f(x)$ (Bias)
Irreducible Error:
- Source 3: how $y$ differs from “true” $f(x)$

Bias-Variance Trade-off: Example

For now: focus on regression problems (ideas extend to classification)
Consider: three different examples of simulated “toy” datasets and three types of models ($\hat{f}_i(.)$)
- Linear Regression orange
- Smoothing Spline 1 blue
- More flexible Smoothing Spline 2 green
“True” (simulated) function $f(.)$ black
Training Error
Test Error

Bias-Variance Trade-off: Example

From ISLR2

Bias-Variance Trade-off: Example

From ISLR2

Bias-Variance Trade-off: Example

From ISLR2

Bias-Variance Trade-off: Example

From ISLR2

Linear Regression

A Familiar Supervised Learning Model

Assume relationship between $\mathbf{X}$ and $Y$ is: \[Y=f(\mathbf{X}) + \epsilon\] where $\epsilon$ is a random error term (includes measurement error, other discrepancies) independent of $\mathbf{X}$ and has mean zero.
Objective: To approximate/estimate $f(\mathbf{X})$
Linear Regression: assume that $f(\mathbf{X})$ is a linear function of $\mathbf{X}$
- For $p=1$: $f(\mathbf{X}) = \beta_0 + \beta_1 X_1$
- For $p > 1$: $f(\mathbf{X}) = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p$

Linear Regression

Suppose the CEO of a restaurant franchise is considering opening new outlets in different cities. They would like to expand their business to cities that give them higher profits with the assumption that highly populated cities will probably yield higher profits.

They have data on the population (in 100,000) and profit (in $1,000) at 97 cities where they currently have outlets.

outlets <- readRDS("../data/outlets.rds")   # load dataset
head(outlets) |> kable() # first six observations of the dataset

population	profit
6.1101	17.5920
5.5277	9.1302
8.5186	13.6620
7.0032	11.8540
5.8598	6.8233
8.3829	11.8860

Linear Regression

Objective: choose “best” $\beta_0$ and $\beta_1$ if we assume \[\text{profit} = \beta_0 + \beta_1\times\text{population}\]
Once this is done, we can:
- predict the profit for a new city with a given population
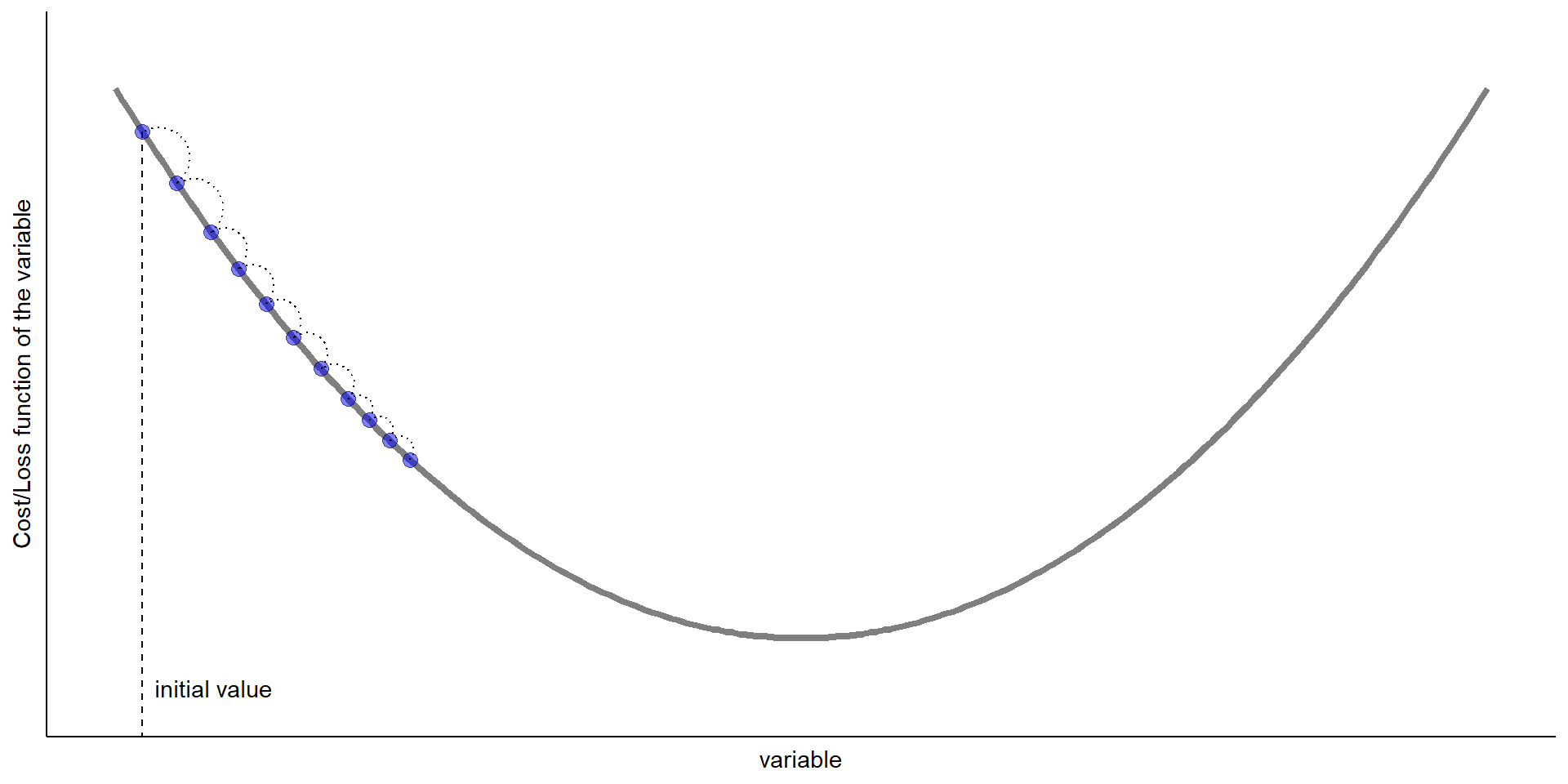
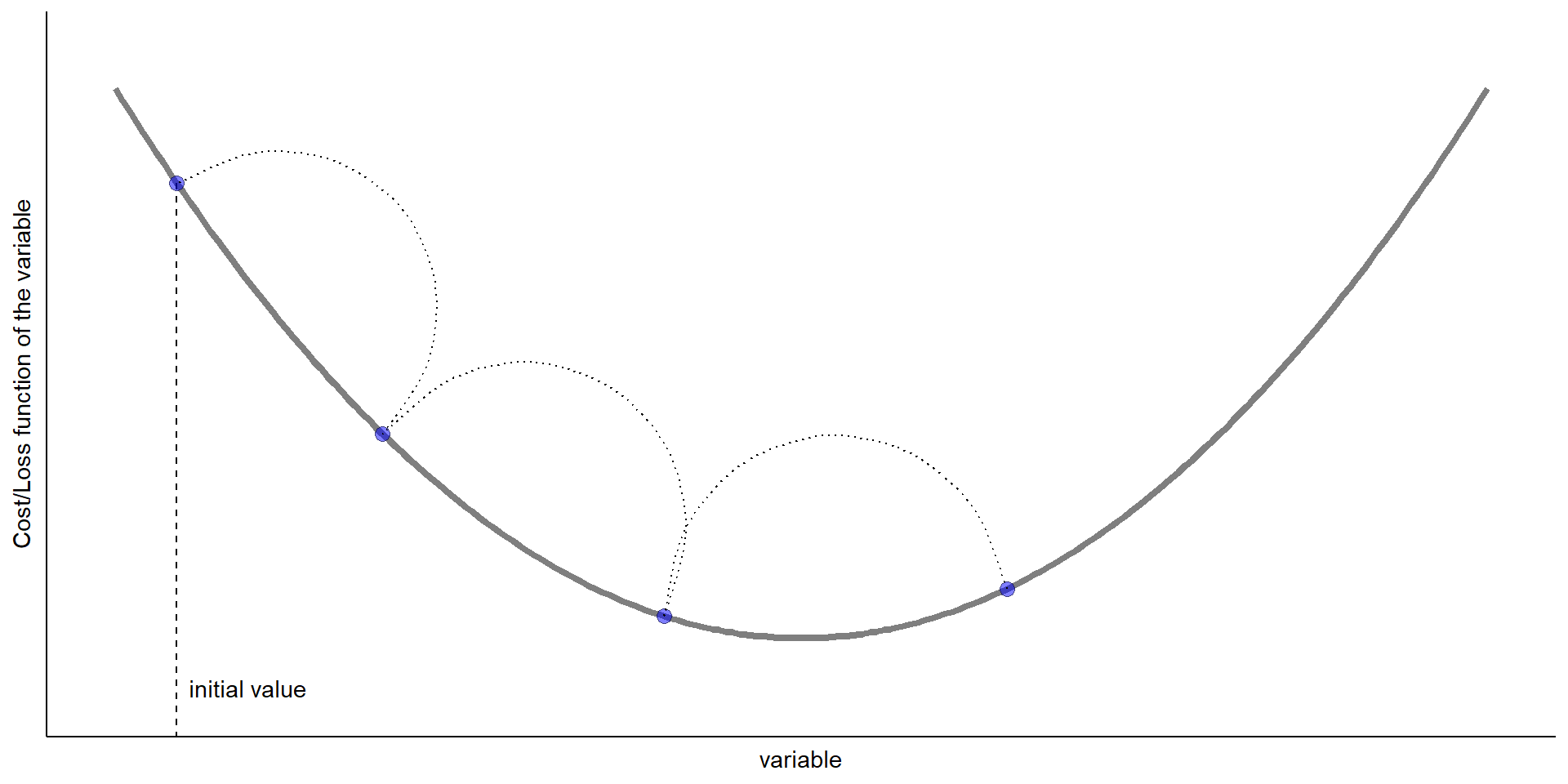
- understand the relationship between population and profit better

Outlet EDA

outlets |> ggpairs() # ggpairs is from GGAlley package

Linear Regression: Estimating Parameters

Suppose we have $\hat{\beta}_0$ and $\hat{\beta}_1$
Observed response: $y_i$ for $i=1,\ldots,n$
Predicted response: $\hat{y}_i$ for $i=1, \ldots, n$
Residual: $e_i = \hat{y}_i - y_i$ for $i=1, \ldots, n$
Mean Squared Error (MSE): $MSE =\dfrac{e^2_1+e^2_2+\ldots+e^2_n}{n}$ also known as the loss/cost function
GOAL: Find $\hat{\beta}_0$ and $\hat{\beta}_1$ which minimizes $MSE$

Gradient Descent Algorithm

How do we minimize the $MSE$?
- Can be done “analytically” but most ML models can’t be fit that way
Today: popular optimization algorithm called gradient descent.
NOTE: Gradient Descent is not a machine learning model/algorithm. It is an optimization technique that helps to fit machine learning models.

Gradient Descent Algorithm

Think of the MSE as a function of $\hat{\beta}_0$ and $\hat{\beta}_1$
- $\text{MSE} = \frac{\sum (y_i - \hat{\beta}_0 - \hat{\beta}_1)^2}{n}$

Gradient Descent Algorithm

Updates to the parameter: \[ \begin{aligned} \text{new value of parameters} &= \text{old value of parameters}\\ &\qquad- \text{step size} \times \text{gradient of function w.r.t. parameters} \end{aligned} \]

Gradient Descent Algorithm

Gradient Descent for Linear Regression

Objective: We want to find $\hat{\beta}_0$ and $\hat{\beta}_1$ which minimizes
\[\begin{aligned} MSE &= \dfrac{e^2_1+e^2_2+\ldots+e^2_n}{n}\\ &= \dfrac{(\hat{y}_1 - y_1)^2 + (\hat{y}_2 - y_2)^2 + \ldots + (\hat{y}_n - y_n)^2}{n} \end{aligned}\]
\[MSE = \dfrac{(\hat{\beta}_0 + \hat{\beta}_1 \ x_1 - y_1)^2 + (\hat{\beta}_0 + \hat{\beta}_1 \ x_2 - y_2)^2 + \ldots + (\hat{\beta}_0 + \hat{\beta}_1 \ x_n - y_n)^2}{n}\]
\[MSE = \displaystyle \dfrac{1}{n}\sum_{i=1}^{n} (\hat{\beta}_0 + \hat{\beta}_1 \ x_i - y_i)^2 = \displaystyle \dfrac{1}{n}\sum_{i=1}^{n} (\hat{y}_i - y_i)^2 = \displaystyle \dfrac{1}{n}\sum_{i=1}^{n} (e_i)^2\]

Gradient Descent for Linear Regression

To compute gradient, need partial derivatives of $MSE$ with respect to $\hat{\beta}_0$ and $\hat{\beta}_1$.
\[\text{gradient of MSE with respect to} \ \hat{\beta}_0 = \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} (\hat{\beta}_0 + \hat{\beta}_1 \ x_i - y_i) = \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} (\hat{y}_i - y_i)\]
\[\text{gradient of MSE with respect to} \ \hat{\beta}_1 = \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} x_i (\hat{\beta}_0 + \hat{\beta}_1 \ x_i - y_i) = \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} x_i (\hat{y}_i - y_i)\]

Gradient Descent for Linear Regression

Gradient descent update:
- For $\hat{\beta}_0$: \[ \begin{aligned} \hat{\beta}_0 \ \text{(new)} &= \hat{\beta}_0 \ \text{(old)}- \bigg(\text{step size} \times \text{derivative w.r.t} \ \hat{\beta}_0\bigg)\\ &= \hat{\beta}_0 \ \text{(old)}- \bigg(\text{step size} \times \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} (\hat{y}_i - y_i)\bigg) \end{aligned} \]
- For $\hat{\beta}_1$: \[ \begin{aligned} \hat{\beta}_1 \ \text{(new)} &= \hat{\beta}_1 \ \text{(old)} - \bigg(\text{step size} \times \text{derivative w.r.t} \ \hat{\beta}_1 \bigg)\\ &= \hat{\beta}_1 \ \text{(old)} - \bigg(\text{step size} \times \dfrac{2}{n} \displaystyle \sum_{i=1}^{n} x_i (\hat{y}_i - y_i)\bigg) \end{aligned} \]