MAT-427: Multiple Linear Regression + Data Splitting

Eric Friedlander

Computational Setup

library(tidyverse)
library(knitr)
library(readODS)

Question!!!

As a model’s flexibility increases:

  1. its variance (increases/decreases)
  2. its bias (increases/decreases)
  3. its training MSE (increases/decreases)
  4. its test MSE (describe)
  1. its variance (increases)
  2. its bias (decreases)
  3. its training MSE (decreases)
  4. its test MSE (decreases at first, then increases and the model starts to overfit, U-shaped)

Modeling in R

Outlet Data

Suppose the CEO of a restaurant franchise is considering opening new outlets in different cities. They would like to expand their business to cities that give them higher profits with the assumption that highly populated cities will probably yield higher profits.

They have data on the population (in 100,000) and profit (in $1,000) at 97 cities where they currently have outlets.

outlets <- readRDS("../data/outlets.rds")   # load dataset
head(outlets) |> kable() # first six observations of the dataset
population profit
6.1101 17.5920
5.5277 9.1302
8.5186 13.6620
7.0032 11.8540
5.8598 6.8233
8.3829 11.8860

R as an open-source language

  • R is an open source language
    • Advantages:
      • Packages for almost anything you want
      • “Cutting edge” methods rolled out quickly and early
    • Disadvantages
      • Many packages (especially new ones) may have bugs
      • Lots of syntactical diversity
      • Syntax is frequently dependent on the needs of the person who wrote the package and conventions at the time the package was created

Enter tidyverse

The tidyverse is an opinionated collection of R packages designed for data science. All packages share an underlying design philosophy, grammar, and data structures.

  • tidyverse is for manipulating and visualizing data
  • the tidyverse is a meta-package meaning it is a collection of a bunch of other packages

Enter tidymodels

The tidymodels framework is a collection of packages for modeling and machine learning using tidyverse principles.

  • tidymodels creates a unified framework for building models in R
  • Eric’s opinion: similar idea to scikit-learn in Python

Back to linear regression

ggplot(data = outlets) +
  geom_point(mapping = aes(x = population, y = profit)) +    # create scatterplot
  geom_smooth(mapping = aes(x = population, y = profit), 
              method = "lm", se = FALSE)   # add the regression line

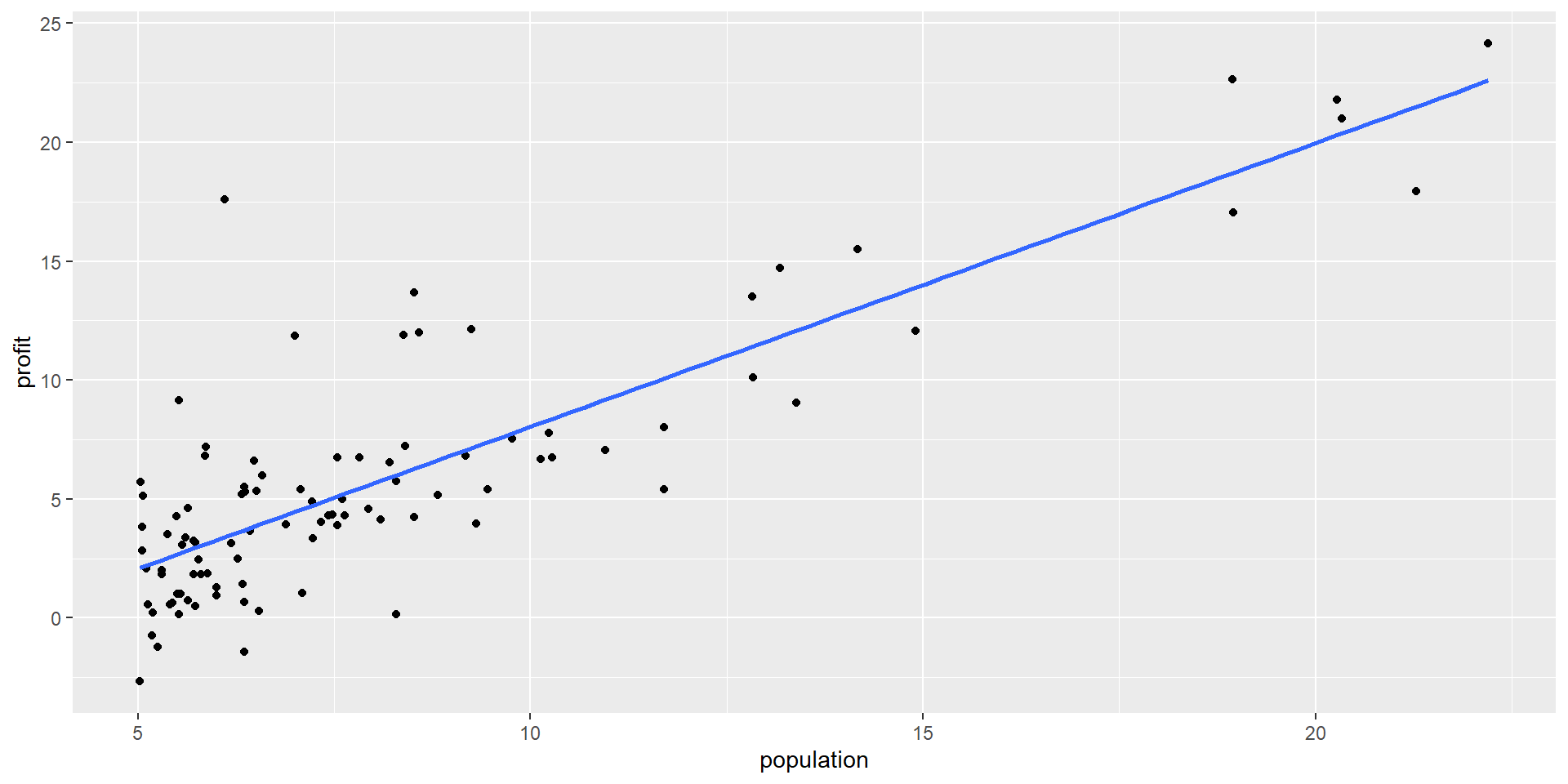
Classic Linear Regression in R

outlets_model <- lm(profit ~ population, data = outlets)
outlets_model

Call:
lm(formula = profit ~ population, data = outlets)

Coefficients:
(Intercept)   population  
     -3.896        1.193

This corresponds to the model:

\[ \begin{aligned} \text{Profit} &= -3.90 + 1.19\times\text{Population}\\ \hat{Y}_i &= -3.90 + 1.19X_i \end{aligned} \] i.e. \(\hat{\beta}_0 = -3.90\) and \(\hat{\beta}_1 = 1.19\)

Modeling with tidymodels

  1. Specify mathematical structure of model (e.g. linear regression, logistic regression)

  2. Specify the engine for fitting the model. (e.g. lm, stan, glmnet).

  3. When required, declare the mode of the model (i.e. regression or classification).

Linear Regression with tidymodels

# Usually put these at the top
library(tidymodels) # load tidymodels package
tidymodels_prefer() # avoid common conflicts

lm_model <- linear_reg() |> # Step 1
  set_engine("lm") # Step 2

# Step 3 not required since linear regression can't be used for classification

# Fit the model
lm_model_fit <- lm_model |> 
  fit(profit ~ population, data = outlets)

Linear Regression with tidymodels

lm_model_fit |> 
  tidy() |> 
  kable()
term estimate std.error statistic p.value
(Intercept) -3.895781 0.7194828 -5.414696 5e-07
population 1.193034 0.0797439 14.960806 0e+00

Same model as before:

\[ \begin{aligned} \text{Profit} &= -3.90 + 1.19\times\text{Population}\\ \hat{Y}_i &= -3.90 + 1.19X_i \end{aligned} \]

Linear Regression in R: Prediction

new_cities <- tibble(population = rnorm(100, 7, 3))

lm_model_fit |> 
predict(new_data = new_cities) |> 
  kable()
.pred
4.2987846
4.3494028
1.6358812
2.8371943
8.6964415
1.2610114
4.4093826
7.0132467
8.9081681
-3.7261162
-0.3152552
-0.0578742
3.1103344
-1.4511631
3.2056127
7.2094157
5.2694317
9.8741950
5.3986612
5.7894116
6.5817409
6.4489003
1.5635853
-5.8145557
0.3096059
4.7217335
8.0782299
6.4065191
7.0495725
10.5119132
3.2281542
5.3756384
10.5424872
2.6444235
3.1483294
5.7659904
3.3551593
-1.1774409
9.5361487
-0.3336581
4.1063193
2.7105932
6.1253040
3.6662178
6.1309169
9.2088409
-2.1660582
4.9800410
5.5140171
3.3714057
5.0758817
2.9767839
4.4891785
-2.2982990
-2.0242922
4.4403419
4.0335077
6.8410161
3.6835670
-0.6670421
6.1270222
7.1611647
3.2563676
11.3135720
-0.8720586
7.4979481
5.4139803
7.3006650
3.3803037
5.1760916
4.7255493
5.3377241
8.0237716
5.0616701
-1.7427836
5.5563838
9.1823534
3.3094120
4.7223157
3.3083360
4.0882384
-0.3834378
0.9586050
6.1677633
-0.9134436
6.9813206
-1.8743103
10.6155073
1.7708313
10.9242269
4.7897426
5.2228631
5.1455980
-0.9701960
5.7970445
0.3254730
1.5828592
-1.7630027
-3.9350027
8.2198551 
new_cities <- tibble(population = rnorm(100, 7, 3))

new_cities <- new_cities |> 
  bind_cols(predict(lm_model_fit, new_data = new_cities, type = "pred_int")) |> 
  kable()

Note: New data must be a data frame with the same columns names as the training data

Multiple Linear Regression

Multiple Linear Regression

  • Response: \(Y\)
  • Predictor Variables: \(X_1, X_2, \ldots, X_p\)
  • Assume true relationship:

\[ \begin{aligned} Y&=f(\mathbf{X}) + \epsilon\\ &=\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \epsilon \end{aligned} \] where \(\beta_j\) quantifies the association between the \(j^{th}\) predictor and the response.

Multiple Linear Regression: Estimating Parameters

  • Suppose \(\hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_p\) are estimates of \(\beta_0, \beta_1, \ldots, \beta_p\)
  • Training Data:
    • Observed response: \(y_i\) for \(i=1,\ldots,n\)
    • Observed predictors: \(x_{1i}, x_{2i}, \ldots x_{pi}\) for \(i=1,\ldots, n\)
  • Predicted response: \[\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1x_{1i} + \ldots + \hat{\beta}_px_{pi} \text{ for } i=1, \ldots, n\]
  • Residuals: \(e_i = \hat{y}_i - y_i\) for \(i=1, \ldots, n\)
  • Mean Squared Error (MSE): \(MSE =\dfrac{e^2_1+e^2_2+\ldots+e^2_n}{n}\)

Multiple Linear Regression: Estimating Parameters

  • Goal: Use training data to find \(\hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_p\) that minimizes MSE
    • \(\hat{\beta}_i\)’s called least-squares estimators
    • Since minimizing MSE \(\implies\) MSE is called cost/loss function
  • Can use calculus or gradient descent to find \(\hat{\beta}_i\)’s

House Prices dataset

  • size is in square feet
  • num_bedrooms is a count
  • price is in $1,000’s
house_prices <- readRDS("../data/house_prices.rds")   # load dataset
head(house_prices, 6) |> kable()  # print first 6 observations
size num_bedrooms price
2104 3 399.9
1600 3 329.9
2400 3 369.0
1416 2 232.0
3000 4 539.9
1985 4 299.9

Multiple Linear Regression

Some Exploratory Data Analysis (EDA)

library(GGally)
ggpairs(data = house_prices)   # correlation plot

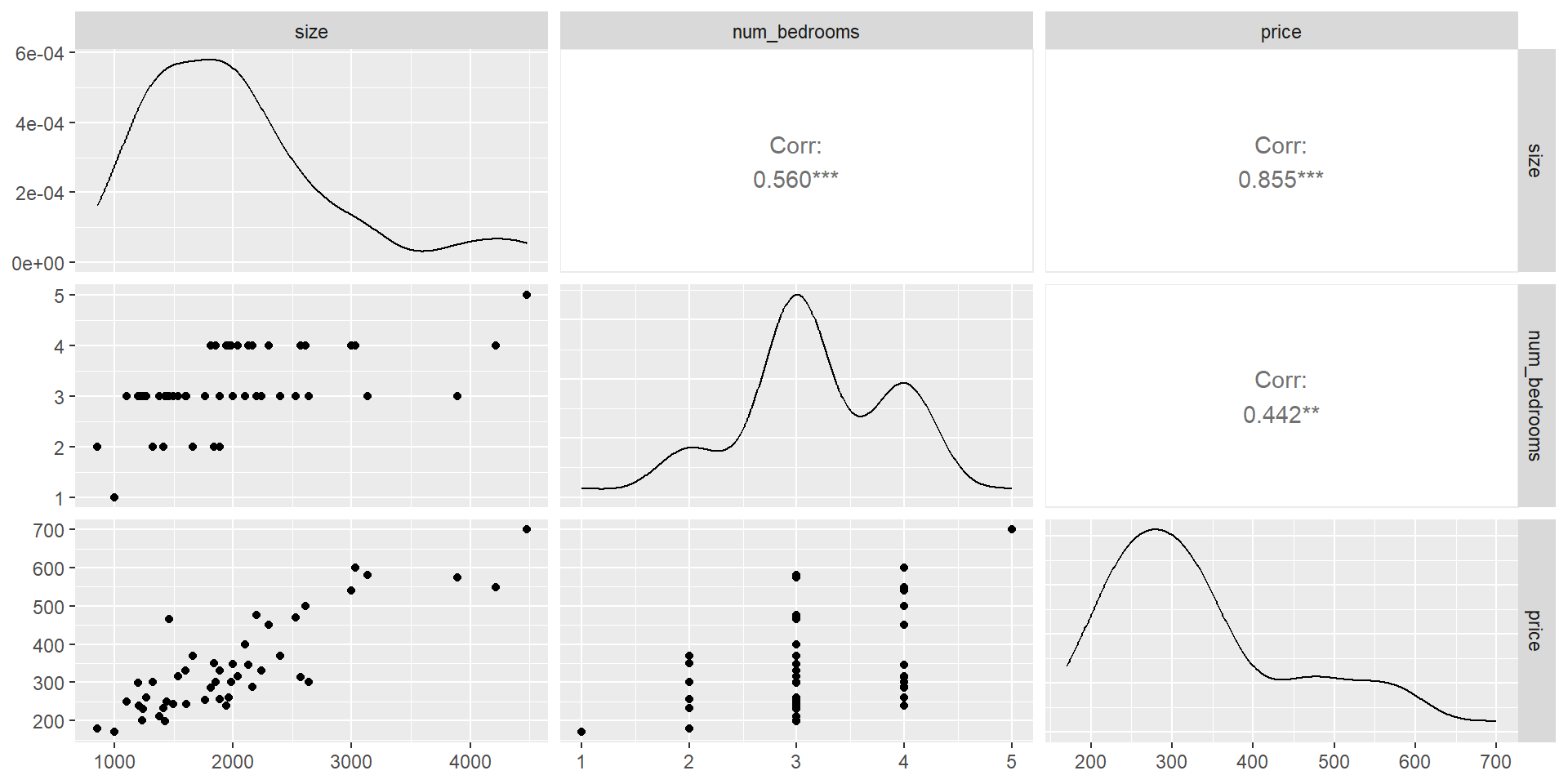
Multiple Linear Regression in R

mlr_model <- linear_reg() |> 
  set_engine("lm")

house_price_mlr <- mlr_model |> 
  fit(price ~ size + num_bedrooms, data = house_prices)   # fit the model

house_price_mlr |> 
  tidy() |>   # produce result summaries of the model
  kable()
term estimate std.error statistic p.value
(Intercept) 89.5977660 41.7674230 2.1451591 0.0374991
size 0.1392106 0.0147951 9.4092391 0.0000000
num_bedrooms -8.7379154 15.4506975 -0.5655353 0.5745825

Multiple Linear Regression: Interpreting Parameters

  • \(\hat{\beta}_0=89.5978\): The intercept \(\implies\) a house with 0 square feet and 0 bedrooms would cost approximately $89,598.80. Is this meaningful in context? Not really
  • \(\hat{\beta}_1=0.1392\): With num_bedrooms remaining fixed, an additional 1 square foot of size leads to an increase in price by approximately $139.20.
  • \(\hat{\beta}_2=-8.7379\): With size remaining fixed, an additional bedroom leads to an decrease in price of approximately $8,737.90.
  • Hmm…. that’s a little weird…
  • Simpson’s Paradox: when relationship between two variables disappears or reverses when controlling for a third, confounding variable

Multiple Linear Regression: Interpreting Parameters

  • Write down our model in mathematical notation
  • \(\text{price} = 89.5978 + 0.1392\times\text{size} - 8.7379\times\text{num_bedrooms}\)
  • \(Y = 89.5978 + 0.1392X_1 - 8.7379X_2\)

Multiple Linear Regression: Prediction

  • Prediction of price when size is 2000 square feet for a house with 3 bedrooms
  • \(\text{sales} = 89.5978 + 0.1392\times2000 - 8.7379\times3 = 341.7841\)
predict(house_price_mlr, new_data = tibble(size = 2000, num_bedrooms = 3))   # obtain prediction
# A tibble: 1 × 1
  .pred
  <dbl>
1  342.
  • Why don’t these match exactly? rounding

Linear Regression: Comparing Models

  • Many methods for comparing regression models from your regression course
  • Today: Data splitting
  • First: New Data
  • ames housing data
    • Many variables
    • Focus on:
      • Sale_Price: in dollars
      • Gr_Liv_Area: size in square feet
      • Bedroom_AbvGr: number of bedrooms above grade

🔗 MAT 427 - Spring 2025 - Schedule