MATH 427: Classification + Logistic Regression

Eric Friedlander

Classification Problems

• Response \(Y\) is qualitative (categorical).
• Objective: build a classifier \(\hat{Y}=\hat{C}(\mathbf{X})\)
  • assigns class label to a future unlabeled (unseen) observations
  • understand the relationship between the predictors and response
• Two ways to make predictions
  • Class probabilities
  • Class labels

Default Dataset

A simulated data set containing information on ten thousand customers. The aim here is to predict which customers will default on their credit card debt.

library(ISLR2)   # load library
head(Default) |> kable()  # print first six observations

default	student	balance	income
No	No	729.5265	44361.625
No	Yes	817.1804	12106.135
No	No	1073.5492	31767.139
No	No	529.2506	35704.494
No	No	785.6559	38463.496
No	Yes	919.5885	7491.559

We will consider default as the response variable.

Split the data

set.seed(427)

default_split <- initial_split(Default, prop = 0.6, strata = default)
default_split

<Training/Testing/Total>
<6000/4000/10000>

default_train <- training(default_split)
default_test <- testing(default_split)

Summarizing our response variable

library(janitor)
Default |> tabyl(default) |> kable()  # class frequencies

default	n	percent
No	9667	0.9667
Yes	333	0.0333

default_train |> tabyl(default) |> kable()

default	n	percent
No	5796	0.966
Yes	204	0.034

default_test |> tabyl(default) |> kable()

default	n	percent
No	3871	0.96775
Yes	129	0.03225

Data Types in R

Default |> glimpse()

Rows: 10,000
Columns: 4
$ default <fct> No, No, No, No, No, No, No, No, No, No, No, No, No, No, No, No…
$ student <fct> No, Yes, No, No, No, Yes, No, Yes, No, No, Yes, Yes, No, No, N…
$ balance <dbl> 729.5265, 817.1804, 1073.5492, 529.2506, 785.6559, 919.5885, 8…
$ income  <dbl> 44361.625, 12106.135, 31767.139, 35704.494, 38463.496, 7491.55…

• fct = factor which is the data type you want to use for categorical data
• as_factor will typically transform things (including numbers) into factors for you
• chr can also be used but factors are better because they store all possible levels for your categorical data
• factors are helpful for plotting because you can reorder the levels to help you plot things

K-Nearest Neighbors Classifier

• Given a value for \(K\) and a test data point \(x_0\): \[P(Y=j | X=x_0)=\dfrac{1}{K} \sum_{x_i \in \mathcal{N}_0} I(y_i = j)\] where \(\mathcal{N}_0\) is the set of the \(K\) “closest” neighbors.
• For classification: neighbors “vote” for class (unlike in regression where predictions are obtained by averaging) \[P(Y=j | X=x_0)=\text{Proportion of neighbors in class }j\]

K-Nearest Neighbors Classifier: Build Model

knn_default_fit <- nearest_neighbor(neighbors = 10) |>
  set_engine("kknn") |>
  set_mode("classification") |>
  fit(default ~ balance, data = default_train)   # fit 10-nn model

• Why don’t I need to worry about centering and scaling?

K-Nearest Neighbors Classifier: Predictions

• predict with a categorical response: documentation
• Two different ways of making predictions

Predicting a class

knn_class_preds <- predict(knn_default_fit, new_data = default_test, type = "class")   # obtain default class label predictions

knn_class_preds |> head() |> kable()

.pred_class
No
No
No
No
No
No

Predicting a probability

• Can anyone pick-out what’s wrong here? Hint: \(k = 10\)

knn_prob_preds <- predict(knn_default_fit, new_data = default_test, type = "prob")   # obtain predictions as probabilities
knn_prob_preds |> filter(.pred_No*.pred_Yes >0) |> head() |> kable()

.pred_No	.pred_Yes
0.8685	0.1315
0.8685	0.1315
0.8685	0.1315
0.8505	0.1495
0.7105	0.2895
0.4775	0.5225

I’ve been lying to you

• kknn actually takes a weighted average of the nearest neighbors
  • I.e. closer observations get more weight
• To use unweighted KNN need weight_func = "rectangular"

Unweighted KNN

knn_default_unw_fit <- nearest_neighbor(neighbors = 10, weight_fun = "rectangular") |>
  set_engine("kknn") |>
  set_mode("classification") |>
  fit(default ~ balance, data = default_train)   # fit 10-nn model

knn_uw_prob_preds <- predict(knn_default_unw_fit, new_data = default_test, type = "prob")   # obtain predictions as probabilities
knn_uw_prob_preds |> filter(.pred_No*.pred_Yes >0) |> head() |> kable()

.pred_No	.pred_Yes
0.9	0.1
0.9	0.1
0.9	0.1
0.9	0.1
0.7	0.3
0.5	0.5

Logistic Regression

Why Not Linear Regression?

Default_lr <- default_train |> 
  mutate(default_0_1 = if_else(default == "Yes", 1, 0))

lrfit <- linear_reg() |> 
  set_engine("lm") |> 
  fit(default_0_1 ~ balance, data = Default_lr)   # fit SLR

lrfit |> predict(new_data = default_train) |> head() |> kable()

.pred
0.0316011
0.0655518
-0.0065293
0.0274263
0.0451629
0.0327046

Why Not Linear Regression?

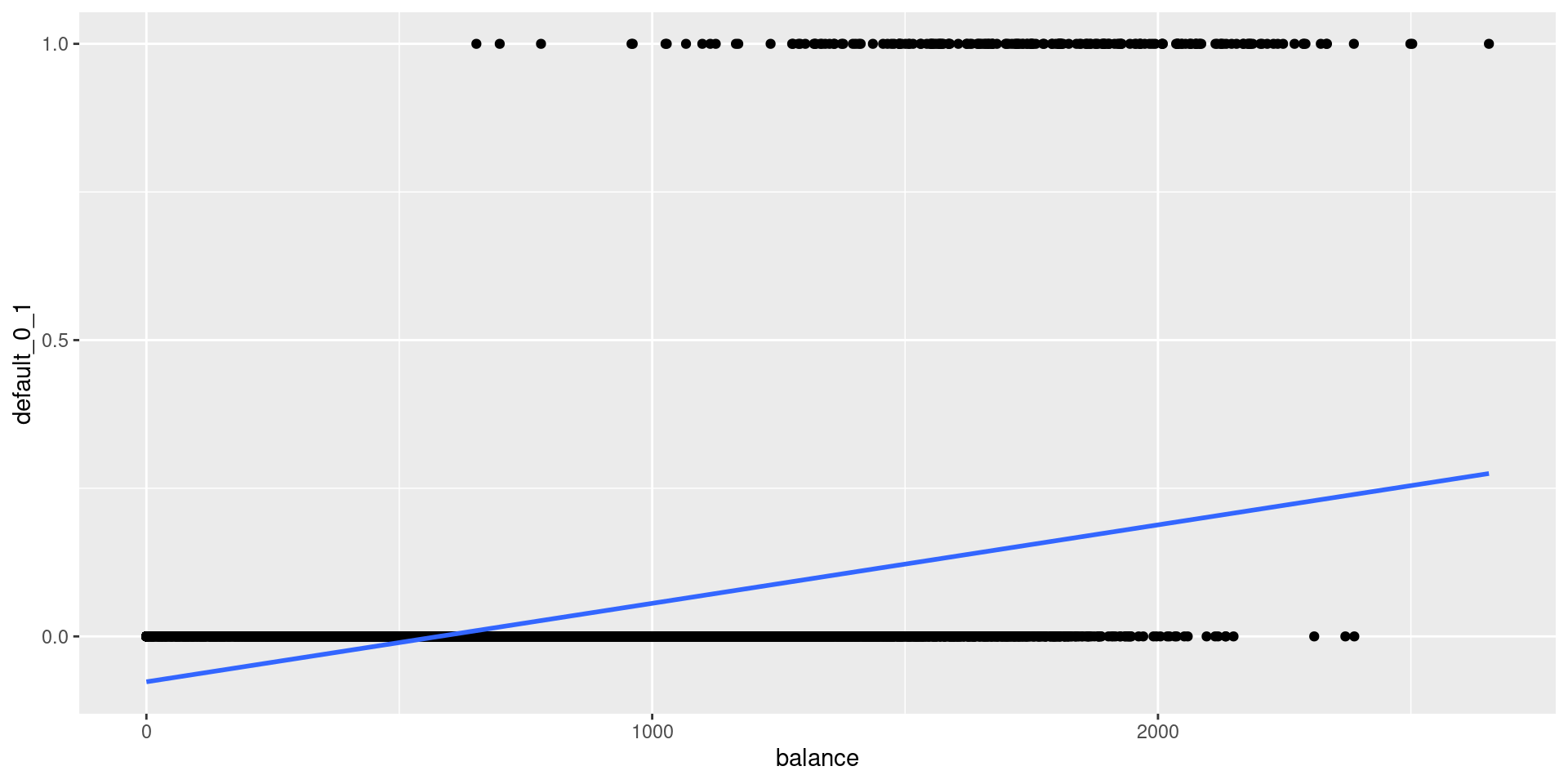
• Linear regression: does not model probabilities well
  • might produce probabilities less than zero or bigger than one
  • treats increase from 0.41 to 0.5 as same as 0.01 to 0.1 (bad)

Why Not Linear Regression?

Suppose we have a response, \[Y=\begin{cases} 1 & \text{if stroke} \\ 2 & \text{if drug overdose} \\ 3 & \text{if epileptic seizure} \end{cases}\]

• Linear regression suggests an ordering, and in fact implies that the differences between classes have meaning
  • e.g. drug overdose \(-\) stroke \(= 1\)? 🤔

Logistic Regression

Consider a one-dimensional binary classification problem:

• Transform the linear model \(\beta_0 + \beta_1 \ X\) so that the output is a probability
• Use logistic function: \[g(t)=\dfrac{e^t}{1+e^t} \ \ \ \text{for} \ t \in \mathcal{R}\]
• Then: \[p(X)=P(Y=1|X)=g\left(\beta_0 + \beta_1 \ X\right)=\dfrac{e^{\beta_0 + \beta_1 \ X}}{1+e^{\beta_0 + \beta_1 \ X}}\]

Other important quantities

• Odds: \(\dfrac{p(x)}{1-p(x)}\)
• Log-Odds (logit): \(\log\left(\dfrac{p(x)}{1-p(x)}\right) = \beta_0 + \beta_1 \ X\)
  • Linear function of predictors

Logistic Regression

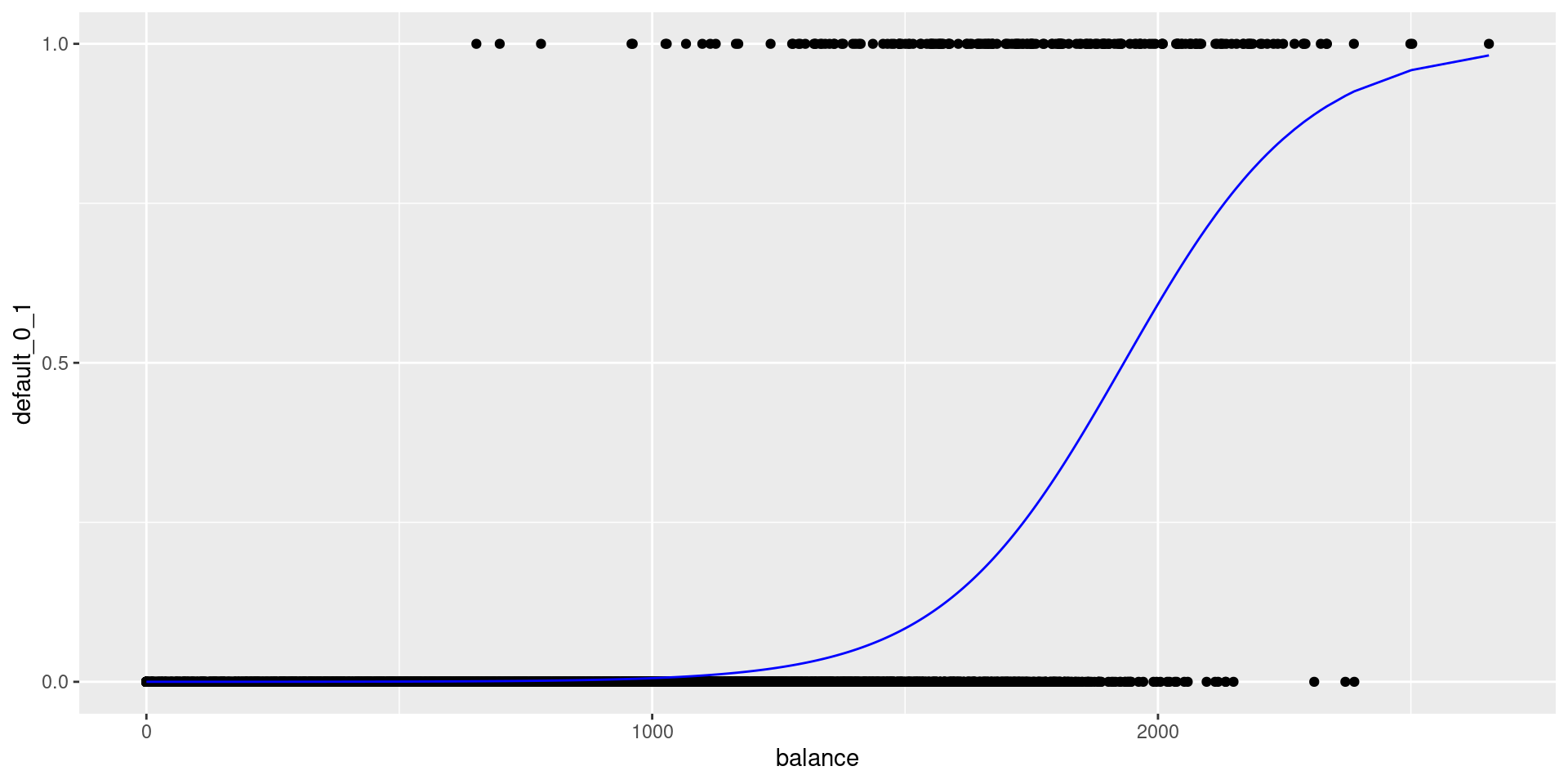
Fitting the model

Fitting a logistic regression model with default as the response and balance as the predictor:

logregfit <- logistic_reg() |> 
  set_engine("glm") |> 
  fit(default ~ balance, data = default_train)   # fit logistic regression model

tidy(logregfit) |> kable()  # obtain results

term	estimate	std.error	statistic	p.value
(Intercept)	-10.6926385	0.4659035	-22.95033	0
balance	0.0055327	0.0002841	19.47329	0

Interpreting Coefficients

• As \(X\) increases by 1, the log-odds increase by \(\hat{\beta}_1\)
  • I.e. probability of default increases but NOT linearly
  • Change in the probability of default due to a one-unit change in balance depends on the current balance value

Interpreting Coefficients

Making predictions: Theory

For balance=$700,

• \[\hat{p}(X)=\dfrac{e^{\hat{\beta}_0+\hat{\beta}_1 X}}{1+e^{\hat{\beta}_0+\hat{\beta}_1 X}}=\dfrac{e^{-10.69 + (0.005533 \times 700)}}{1+e^{-10.69 + (0.005533 \times 700)}}=0.0011\]
• \[\textbf{Odds}(X) = \dfrac{\hat{p}(X)}{1-\hat{p}(X)} = \dfrac{0.0011}{1-0.0011}\approx 0.0011\]
• \[\textbf{Log-Odds}(X)=\log\left(\dfrac{\hat{p}(X)}{1-\hat{p}(X)}\right) = \log(0.0011) = -6.80\]

Making predictions in R

predict(logregfit, new_data = tibble(balance = 700), type = "class") |> kable()   # obtain class predictions

.pred_class
No

predict(logregfit, new_data = tibble(balance = 700), type = "raw") |> kable()   # obtain log-odds predictions

x
-6.819727

predict(logregfit, new_data = tibble(balance = 700), type = "prob") |> kable()  # obtain probability predictions

.pred_No	.pred_Yes
0.9989092	0.0010908