MATH 427: ROC and AUC
Computational Set-Up
Default Dataset
A simulated data set containing information on ten thousand customers. The aim here is to predict which customers will default on their credit card debt.
Split the data
K-Nearest Neighbors Classifier: Build Model
- Response (\(Y\)):
default - Predictor (\(X\)):
balance
K-Nearest Neighbors Classifier: Predictions
Fitting a logistic regression
Fitting a logistic regression model with default as the response and balance as the predictor:
Making predictions in R
Binary Classifiers
- Start with binary classification scenarios
- With binary classification, designate one category as “Success/Positive” and the other as “Failure/Negative”
- If relevant to your problem: “Positive” should be the thing you’re trying to predict/care more about
- Note: “Positive” \(\neq\) “Good”
- For
default: “Yes” is Positive
- Some metrics weight “Positives” more and viceversa
Last Time
- Confusion Matrix
- Metrics based on confusion matrix
- Accuracy
- Recall/Sensitivity
- Precision/PPV
- Specificity
- NPV
- MCC
- F-Measure
- Today: ROC and AUC
Thresholding
Using a threshold
- Step 1: Predict probabilities for all observations
default_test_wprobs <- default_test |>
mutate(
knn_probs = predict(knnfit, new_data = default_test, type = "prob") |> pull(.pred_Yes),
logistic_probs = predict(logregfit, new_data = default_test, type = "prob") |> pull(.pred_Yes)
)
default_test_wprobs |> head() |> kable() # obtain probability predictions| default | student | balance | income | knn_probs | logistic_probs |
|---|---|---|---|---|---|
| No | No | 729.5265 | 44361.63 | 0 | 0.0012842 |
| No | Yes | 808.6675 | 17600.45 | 0 | 0.0019883 |
| No | Yes | 1220.5838 | 13268.56 | 0 | 0.0190870 |
| No | No | 237.0451 | 28251.70 | 0 | 0.0000843 |
| No | No | 606.7423 | 44994.56 | 0 | 0.0006514 |
| No | No | 286.2326 | 45042.41 | 0 | 0.0001107 |
Using a threshold
- Step 1: Predict probabilities for all observations
- Step 2: Set a threshold to obtain class labels (0.5 below)
threshold <- 0.5 # set threshold
default_test_wprobs <- default_test_wprobs |>
mutate(knn_preds = as_factor(if_else(knn_probs > threshold, "Yes", "No")),
logistic_preds = as_factor(if_else(logistic_probs > threshold, "Yes", "No"))
)
default_test_wprobs |> head() |> kable()| default | student | balance | income | knn_probs | logistic_probs | knn_preds | logistic_preds |
|---|---|---|---|---|---|---|---|
| No | No | 729.5265 | 44361.63 | 0 | 0.0012842 | No | No |
| No | Yes | 808.6675 | 17600.45 | 0 | 0.0019883 | No | No |
| No | Yes | 1220.5838 | 13268.56 | 0 | 0.0190870 | No | No |
| No | No | 237.0451 | 28251.70 | 0 | 0.0000843 | No | No |
| No | No | 606.7423 | 44994.56 | 0 | 0.0006514 | No | No |
| No | No | 286.2326 | 45042.41 | 0 | 0.0001107 | No | No |
Using a threshold
- Step 1: Predict probabilities for all observations
- Step 2: Set a threshold to obtain class labels (0.5 below)
threshold <- 0.5 # set threshold
default_test_wprobs <- default_test_wprobs |>
mutate(knn_preds = as_factor(if_else(knn_probs > threshold, "Yes", "No")),
logistic_preds = as_factor(if_else(logistic_probs > threshold, "Yes", "No")))
default_test_wprobs |> head() |> kable()| default | student | balance | income | knn_probs | logistic_probs | knn_preds | logistic_preds |
|---|---|---|---|---|---|---|---|
| No | No | 729.5265 | 44361.63 | 0 | 0.0012842 | No | No |
| No | Yes | 808.6675 | 17600.45 | 0 | 0.0019883 | No | No |
| No | Yes | 1220.5838 | 13268.56 | 0 | 0.0190870 | No | No |
| No | No | 237.0451 | 28251.70 | 0 | 0.0000843 | No | No |
| No | No | 606.7423 | 44994.56 | 0 | 0.0006514 | No | No |
| No | No | 286.2326 | 45042.41 | 0 | 0.0001107 | No | No |
Performance
Low Threshold
threshold <- 0.1 # set threshold
default_test_wprobs <- default_test_wprobs |>
mutate(knn_preds = as_factor(if_else(knn_probs > threshold, "Yes", "No")))
roc_metrics(default_test_wprobs, truth = default, estimate = knn_preds, event_level = "second") |> kable()| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | binary | 0.9060000 |
| sensitivity | binary | 0.7364341 |
| specificity | binary | 0.9116507 |
High Threshold
threshold <- 0.9 # set threshold
default_test_wprobs <- default_test_wprobs |>
mutate(knn_preds = as_factor(if_else(knn_probs > threshold, "Yes", "No"))
)
roc_metrics(default_test_wprobs, truth = default, estimate = knn_preds, event_level = "second") |> kable()| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | binary | 0.9685000 |
| sensitivity | binary | 0.0310078 |
| specificity | binary | 0.9997417 |
Question
- If I want to improve Recall/Sensitivity should I increase or decrease my threshold?
- If I want to improve my Precision/PPV should I increase or decrease my threshold?
ROC Curve
ROC Curve and AUC
- ROC (Receiver Operating Characteristics) curve: popular graphic for comparing different classifiers across all possible thresholds
- Plots the (1-Specificity) along the x-axis and the Sensitivity (true positive rate) along the y-axis
- AUC: area under the AUC curve
- Ideal ROC curve will hug the top left corner
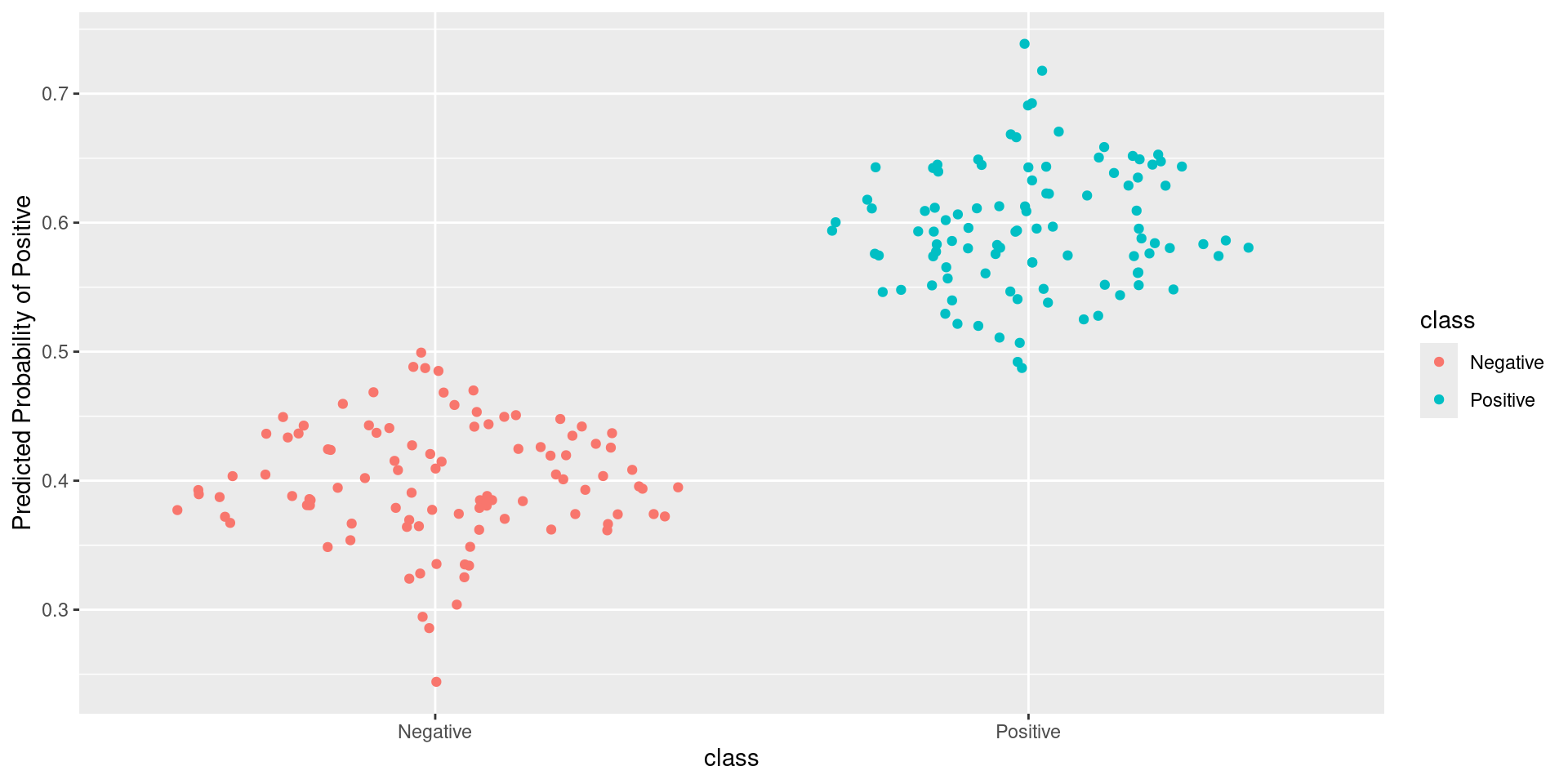
- Idea: How well is my classifier separating positives from negatives
ROC Curve
ROC Curve: Plot

AUC
- AUC: Area under the curve (ROC Curve that is)
- Measures how good your model is at separating categories
- Only for binary classification
AUC in R
Pathological Example 1
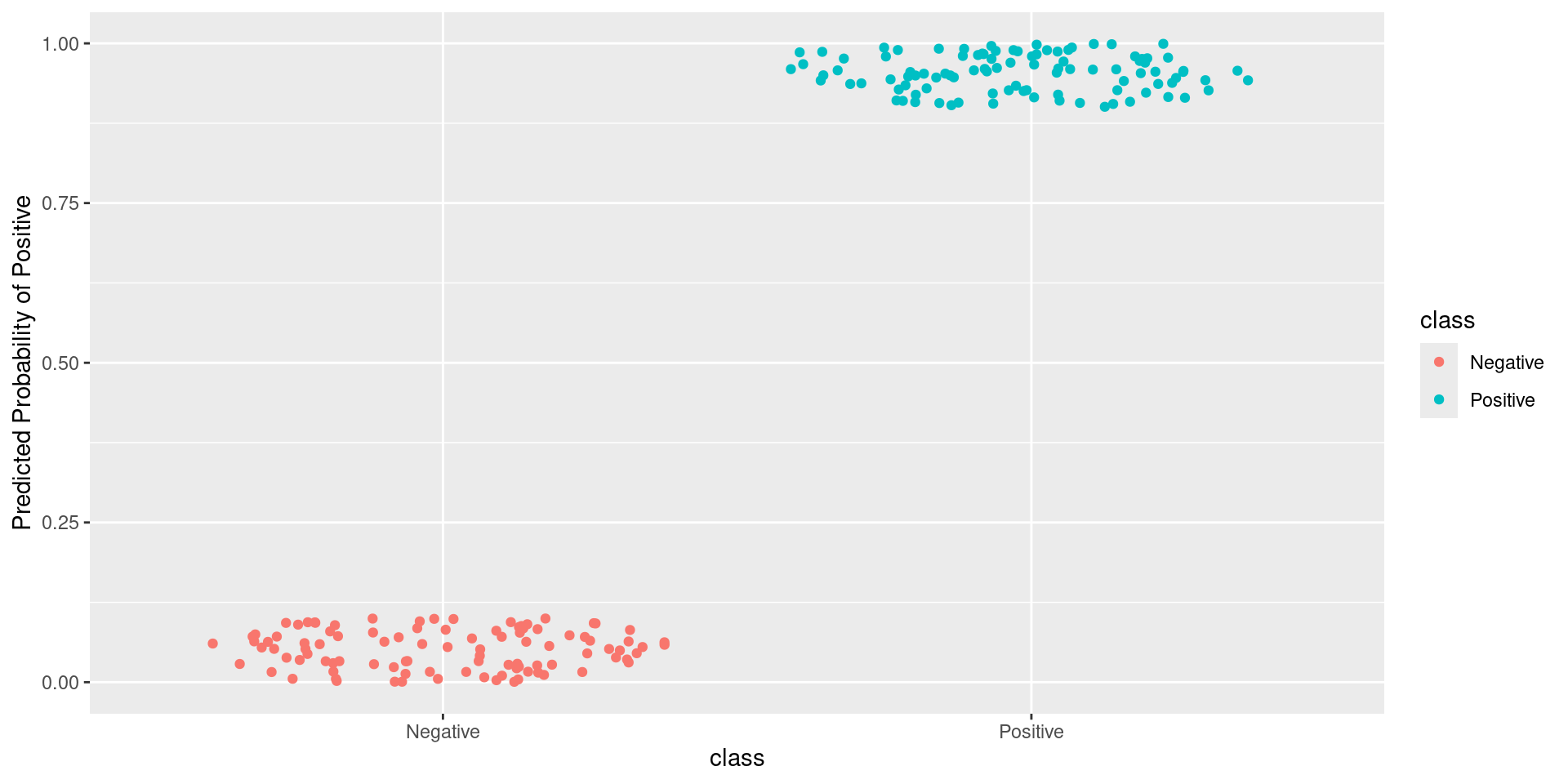
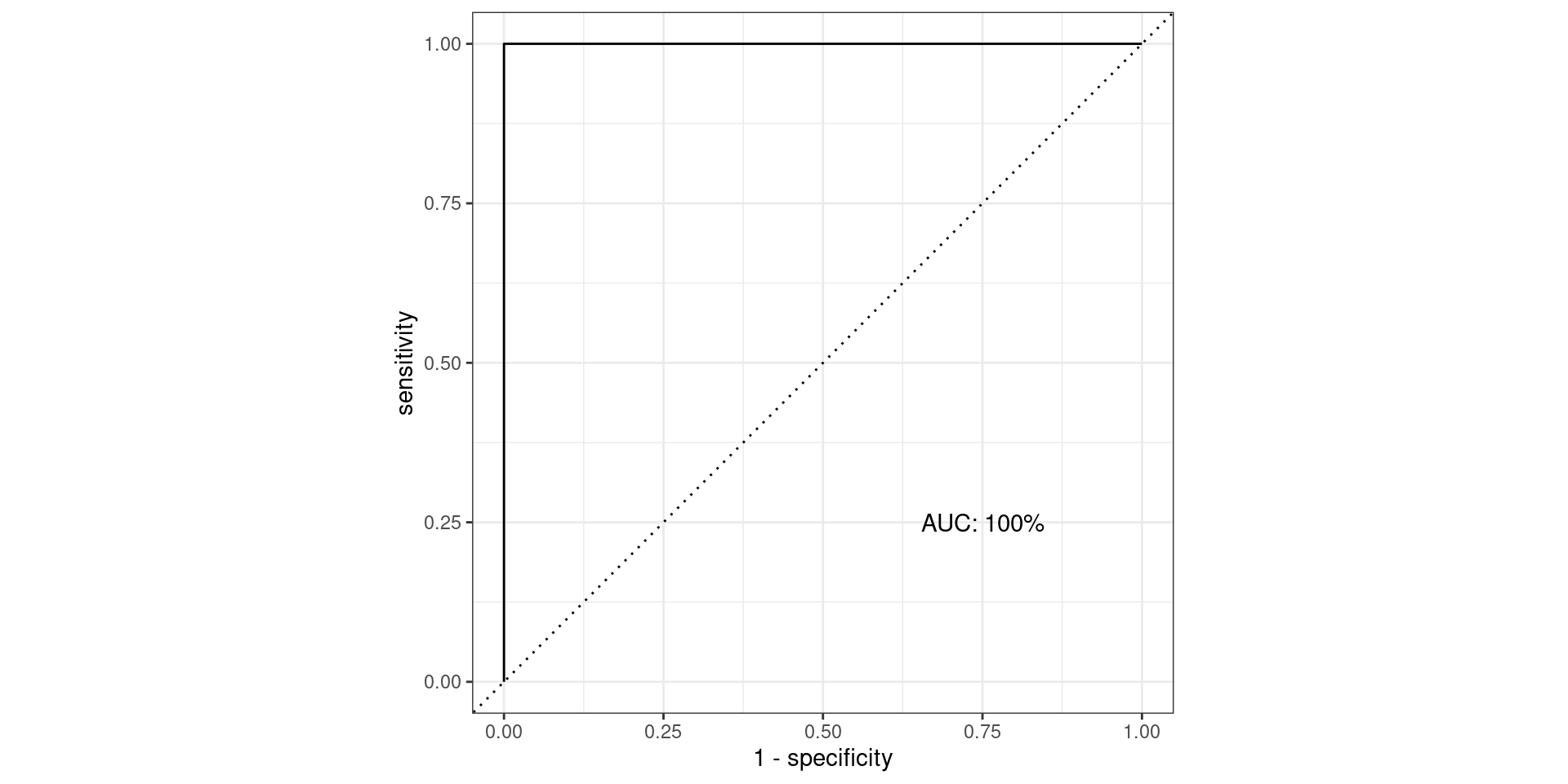
Pathological Example 1
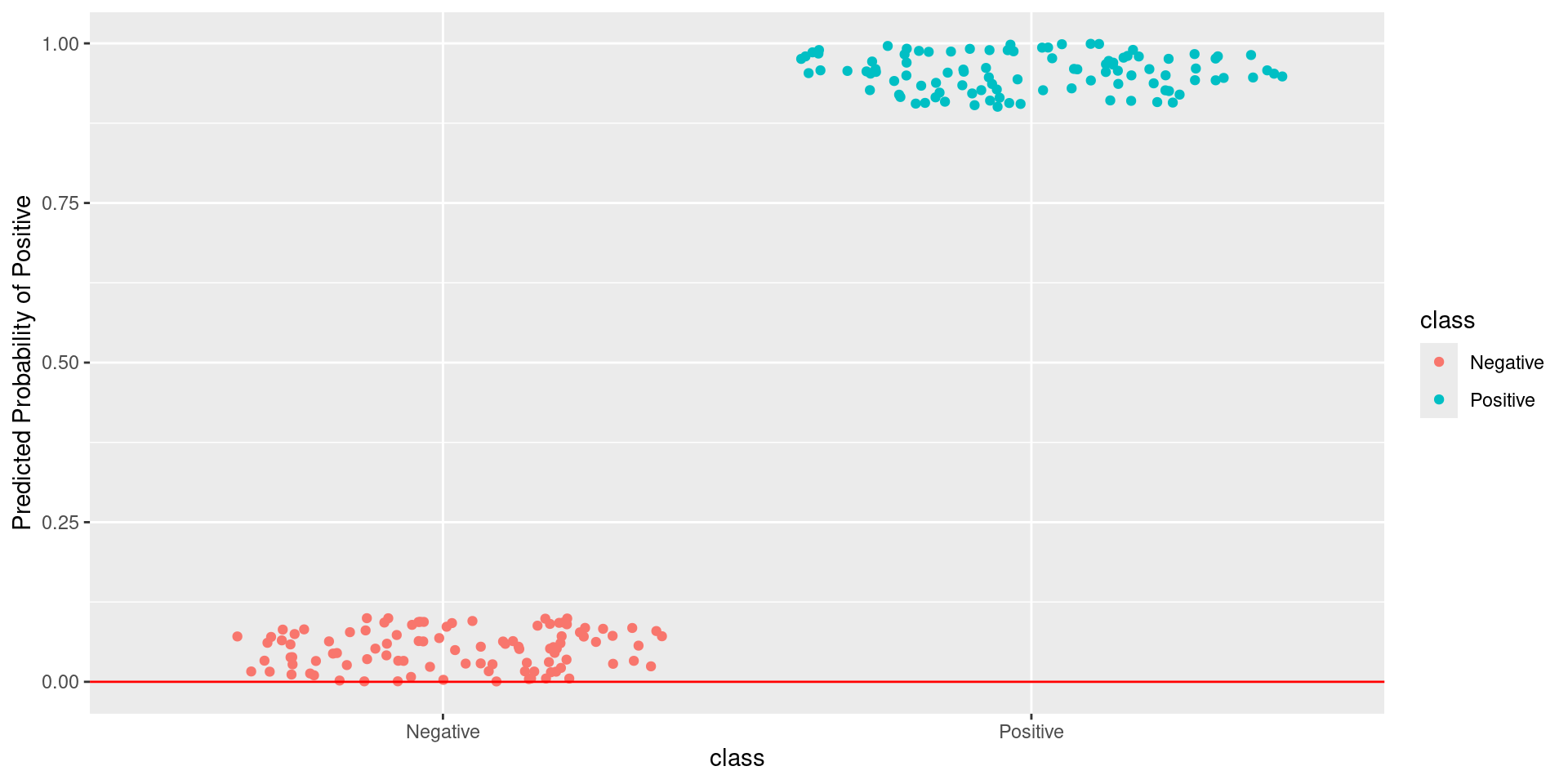
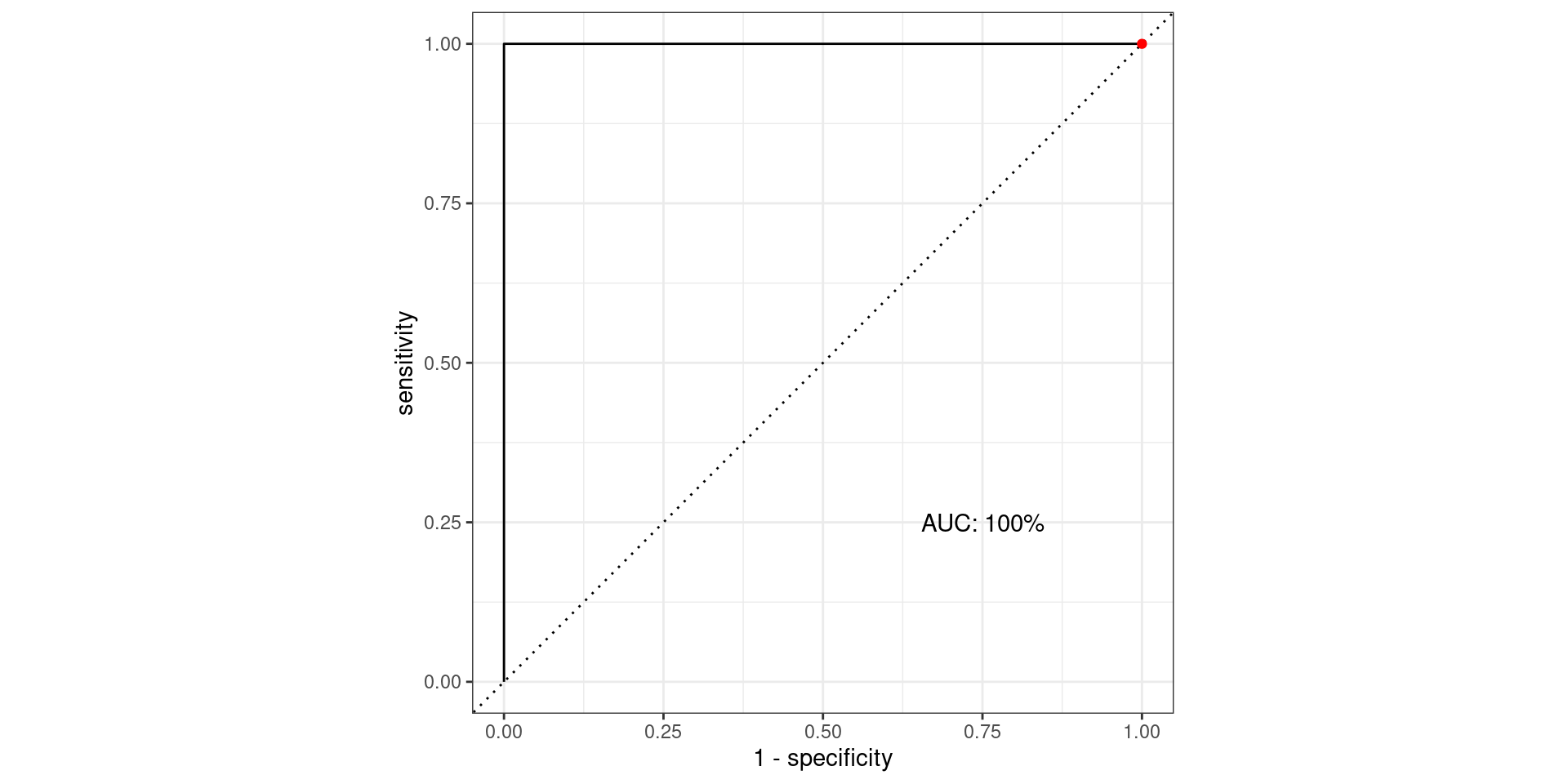
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{100}{100} = 1\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{100}{100} = 1\]
Pathological Example 1
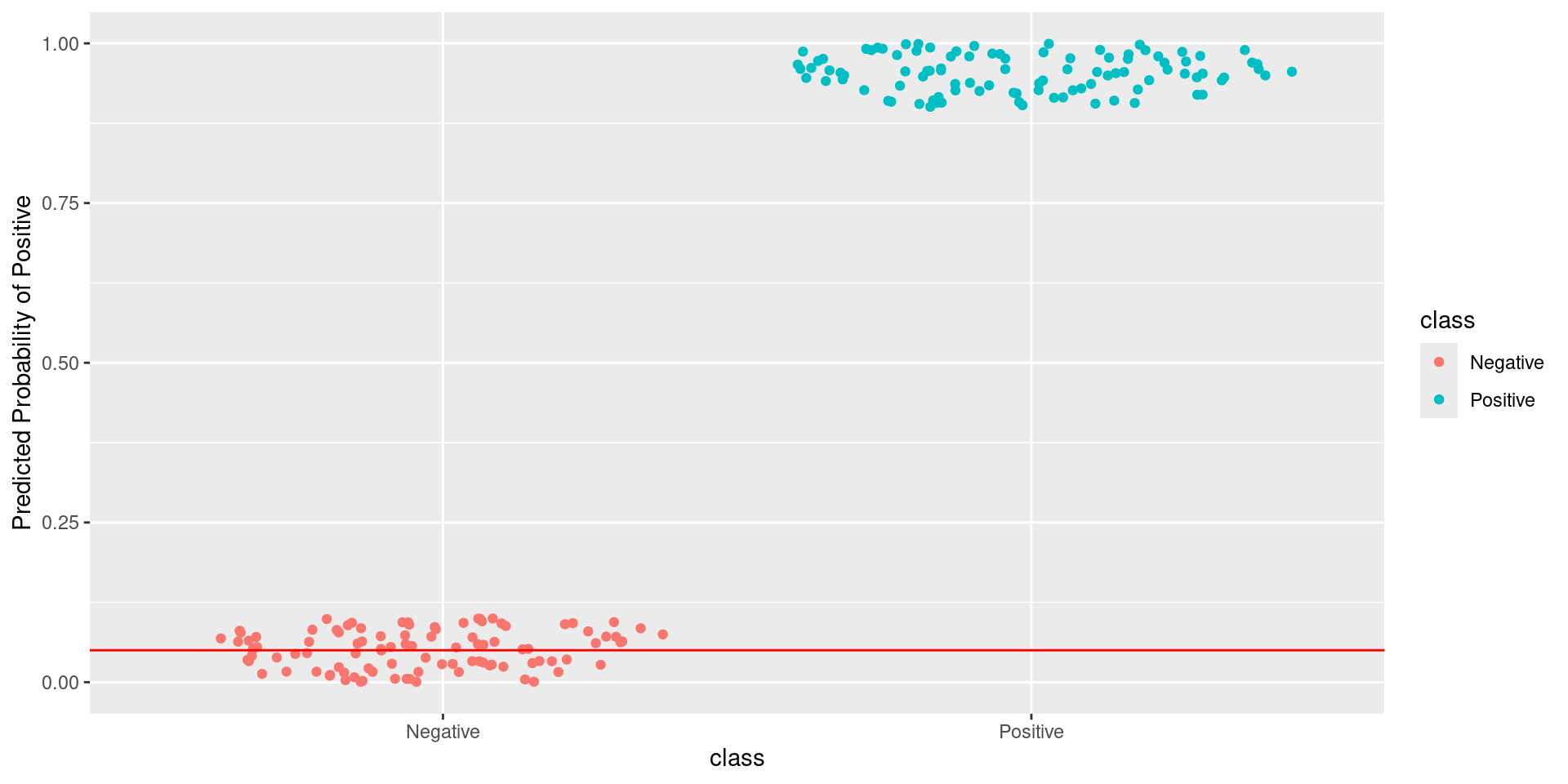
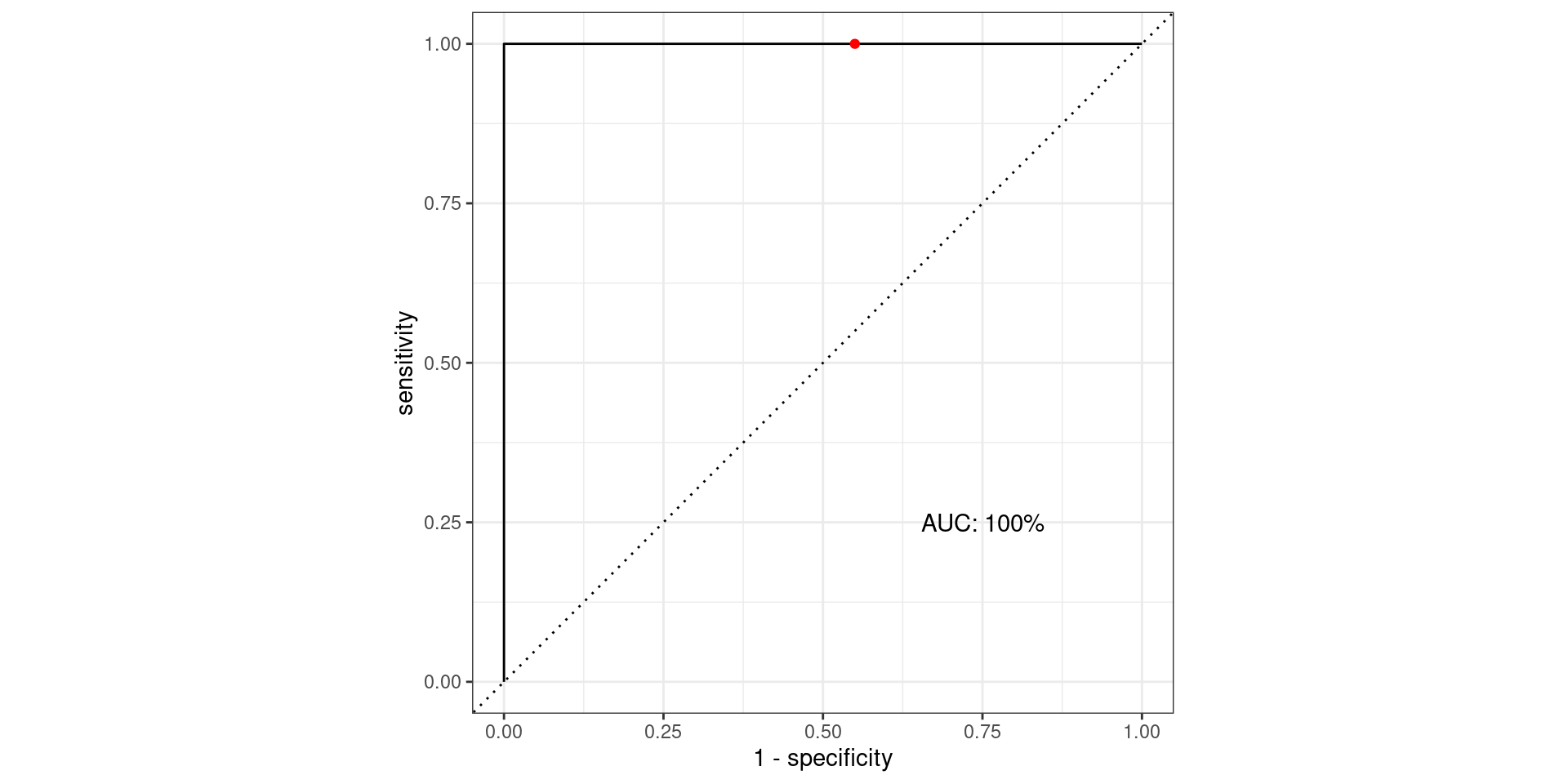
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{100}{100} = 1\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{55}{100} = 0.55\]
Pathological Example 1
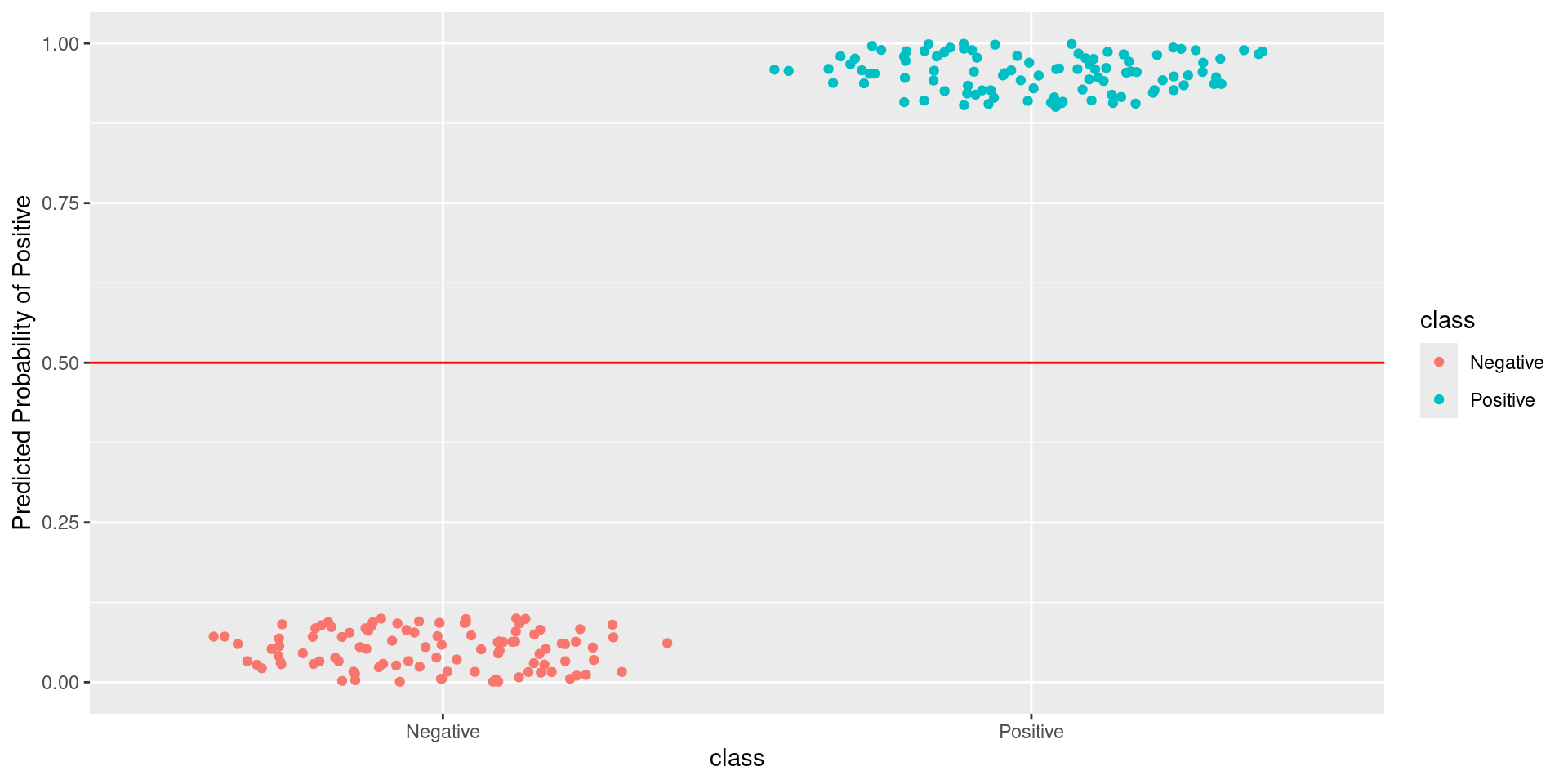
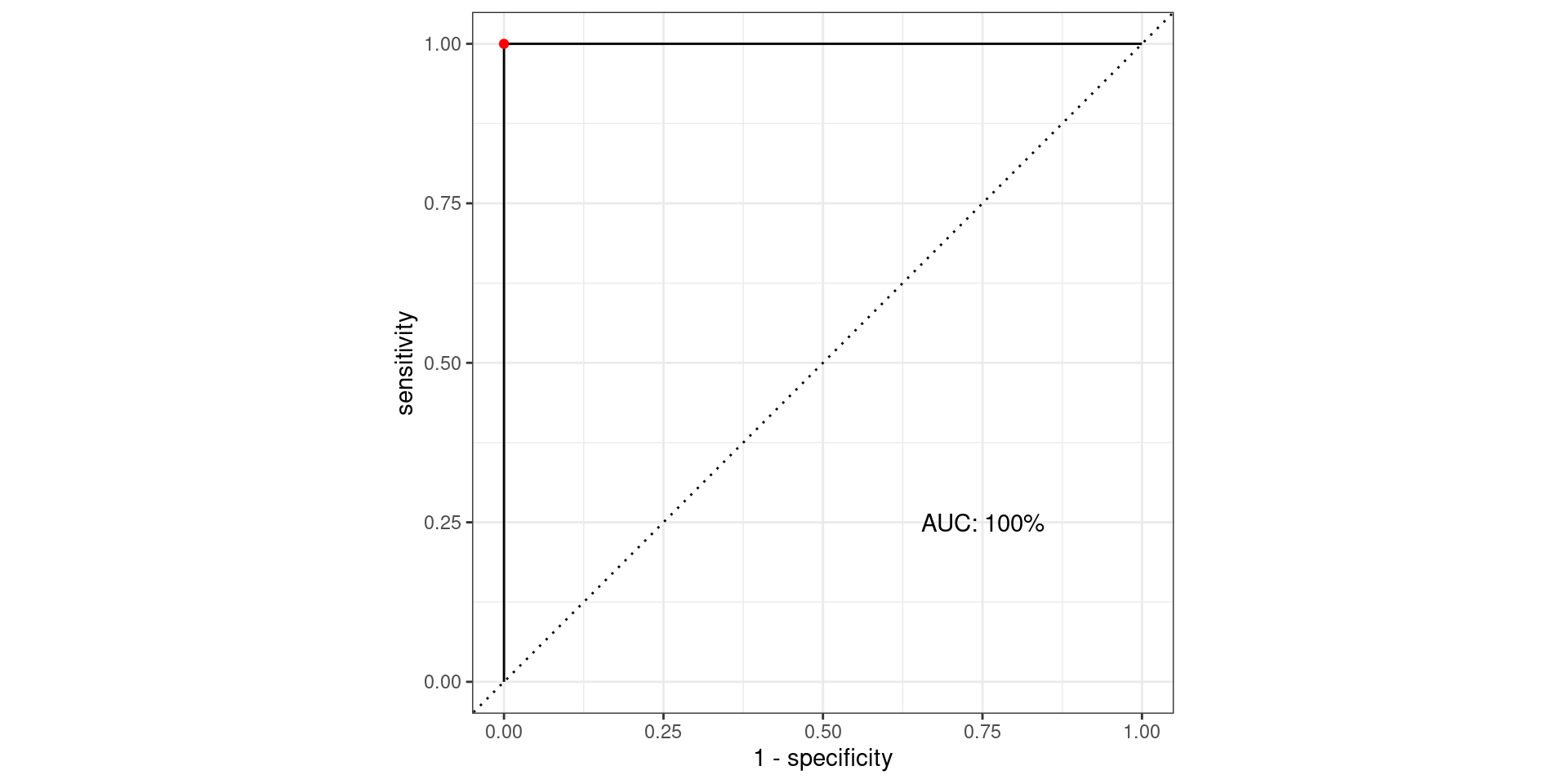
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{100}{100} = 1\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{0}{100} = 0\]
Pathological Example 1
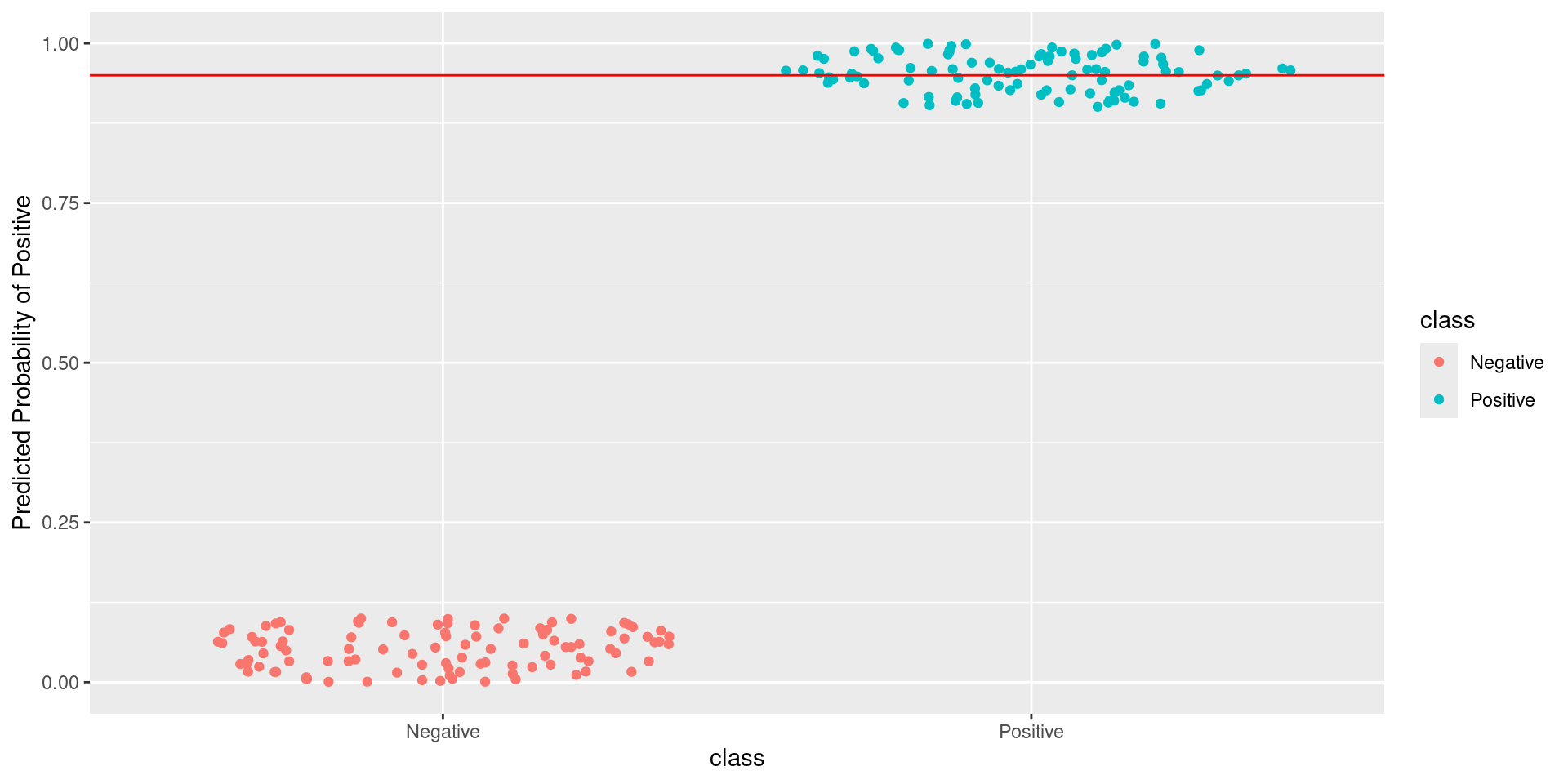
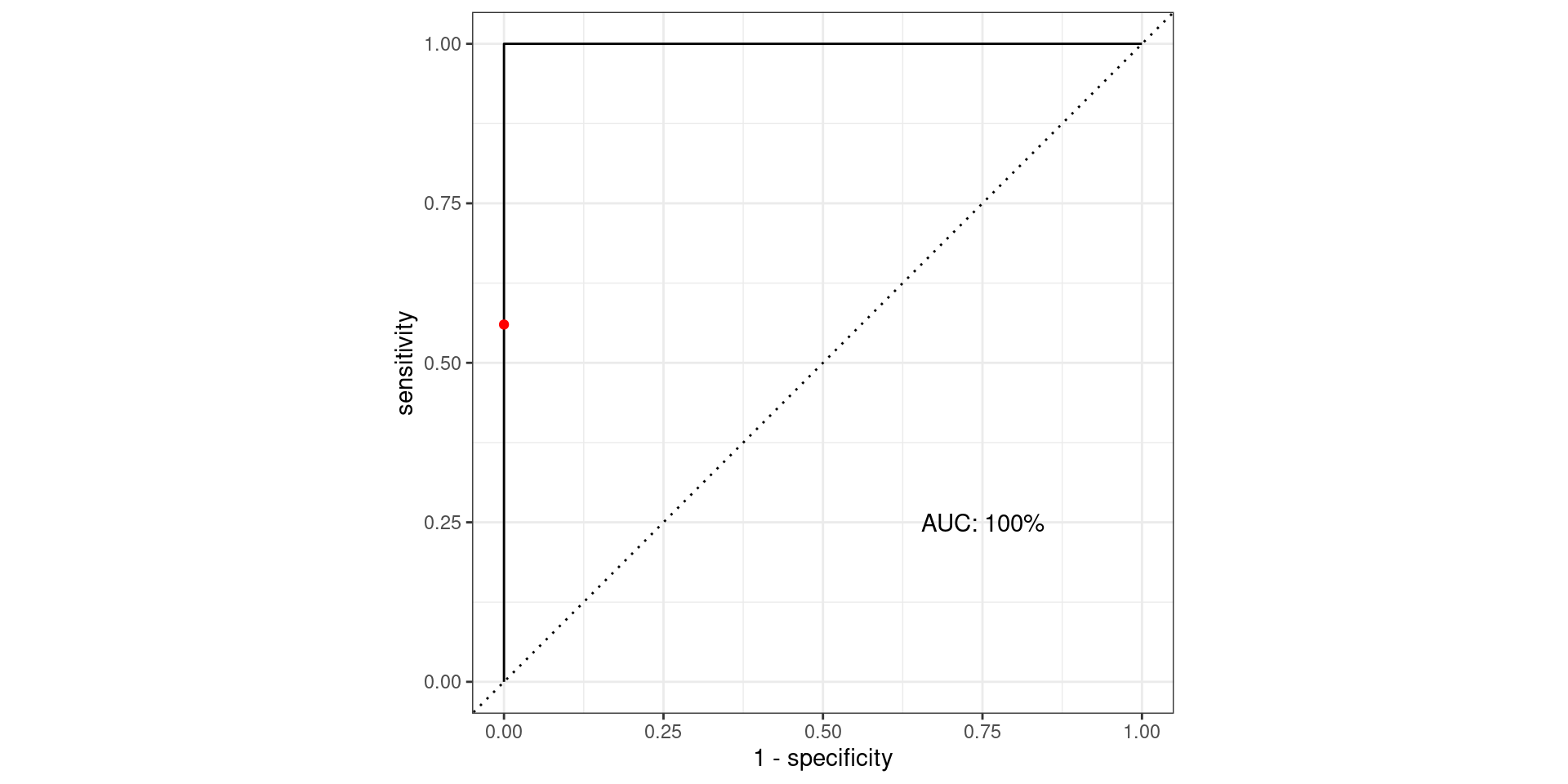
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{56}{100} = 0.56\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{0}{100} = 0\]
Pathological Example 1
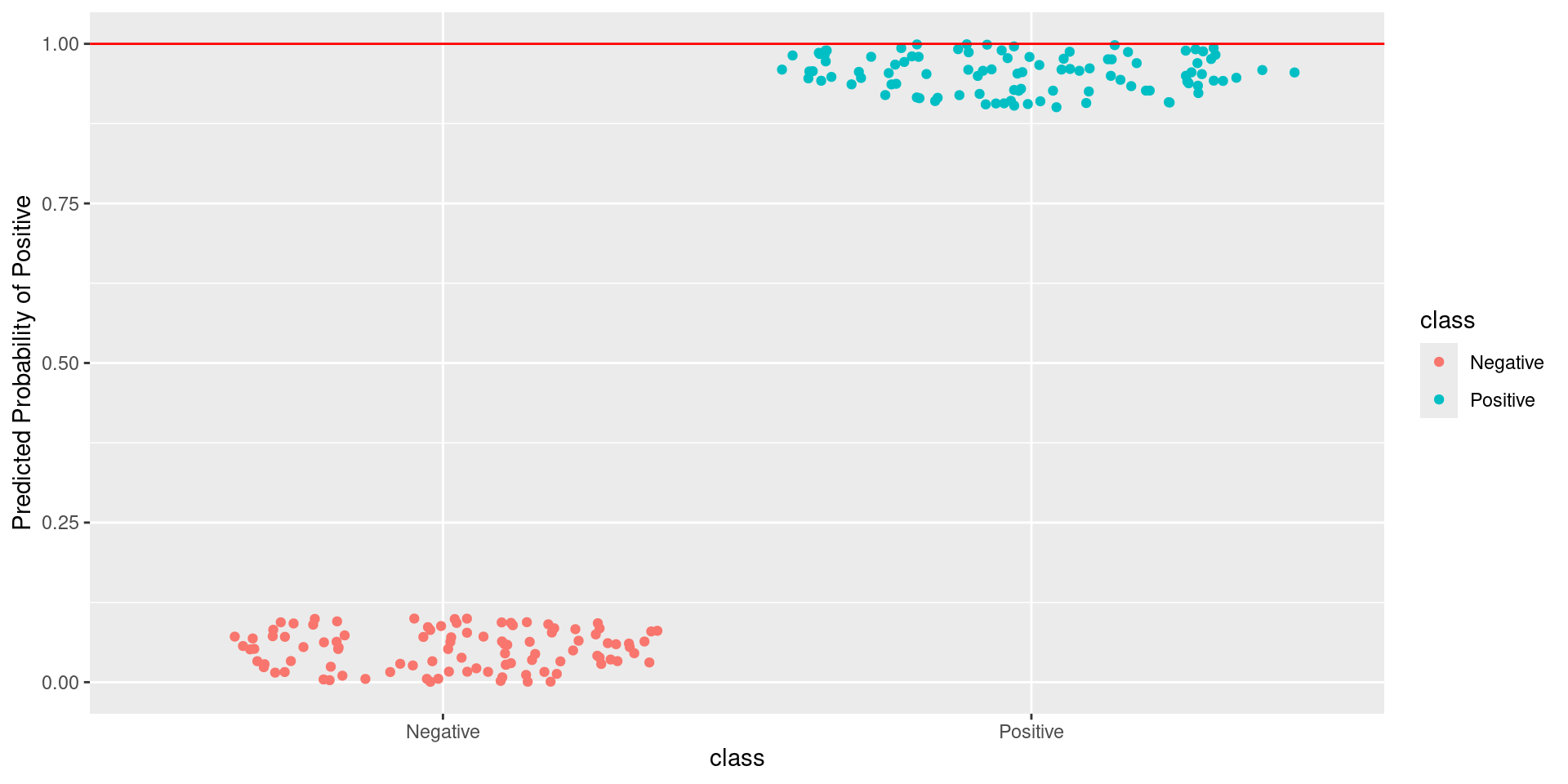
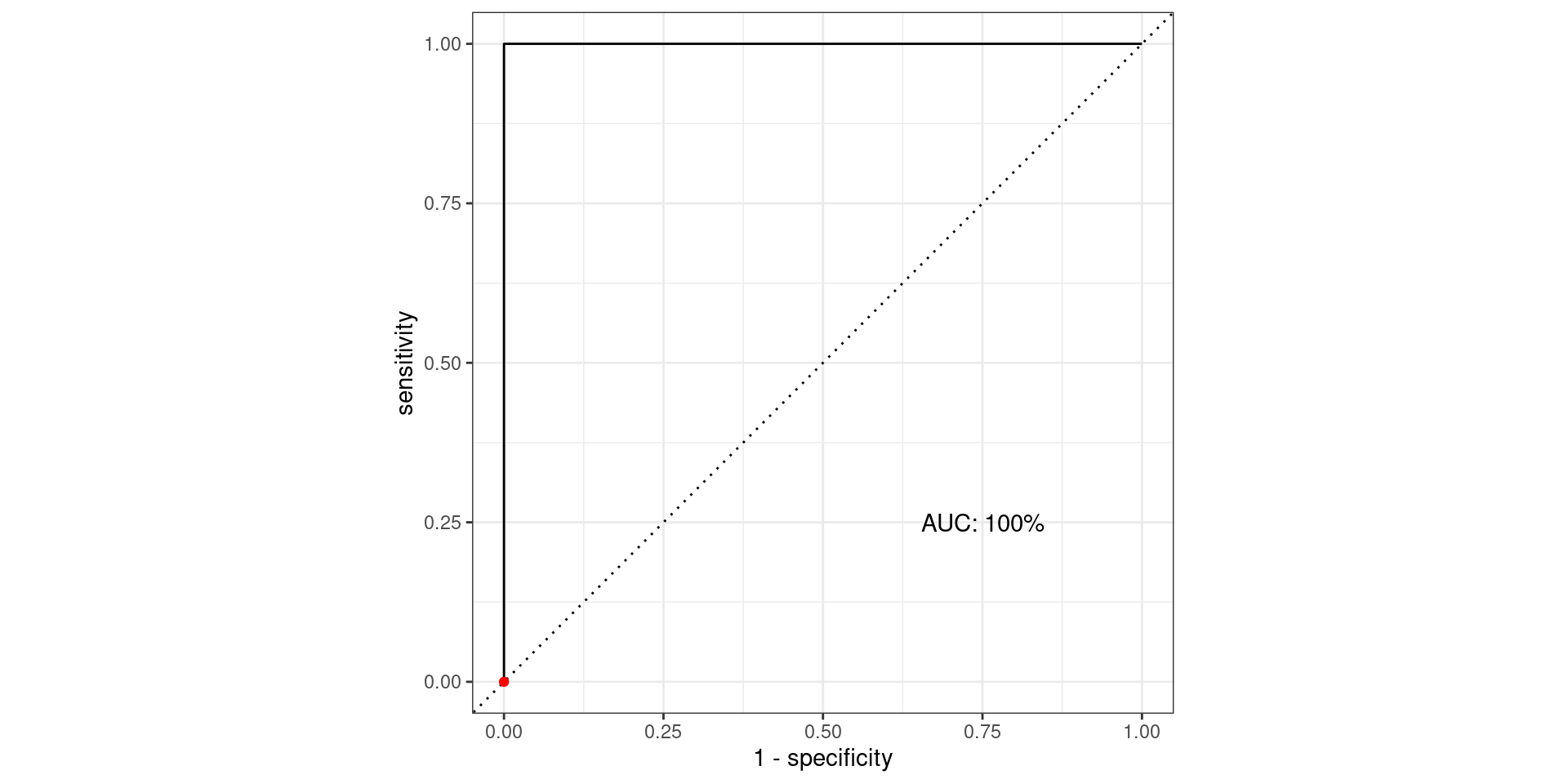
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{0}{100} = 0\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{0}{100} = 0\]
Pathological Example 2
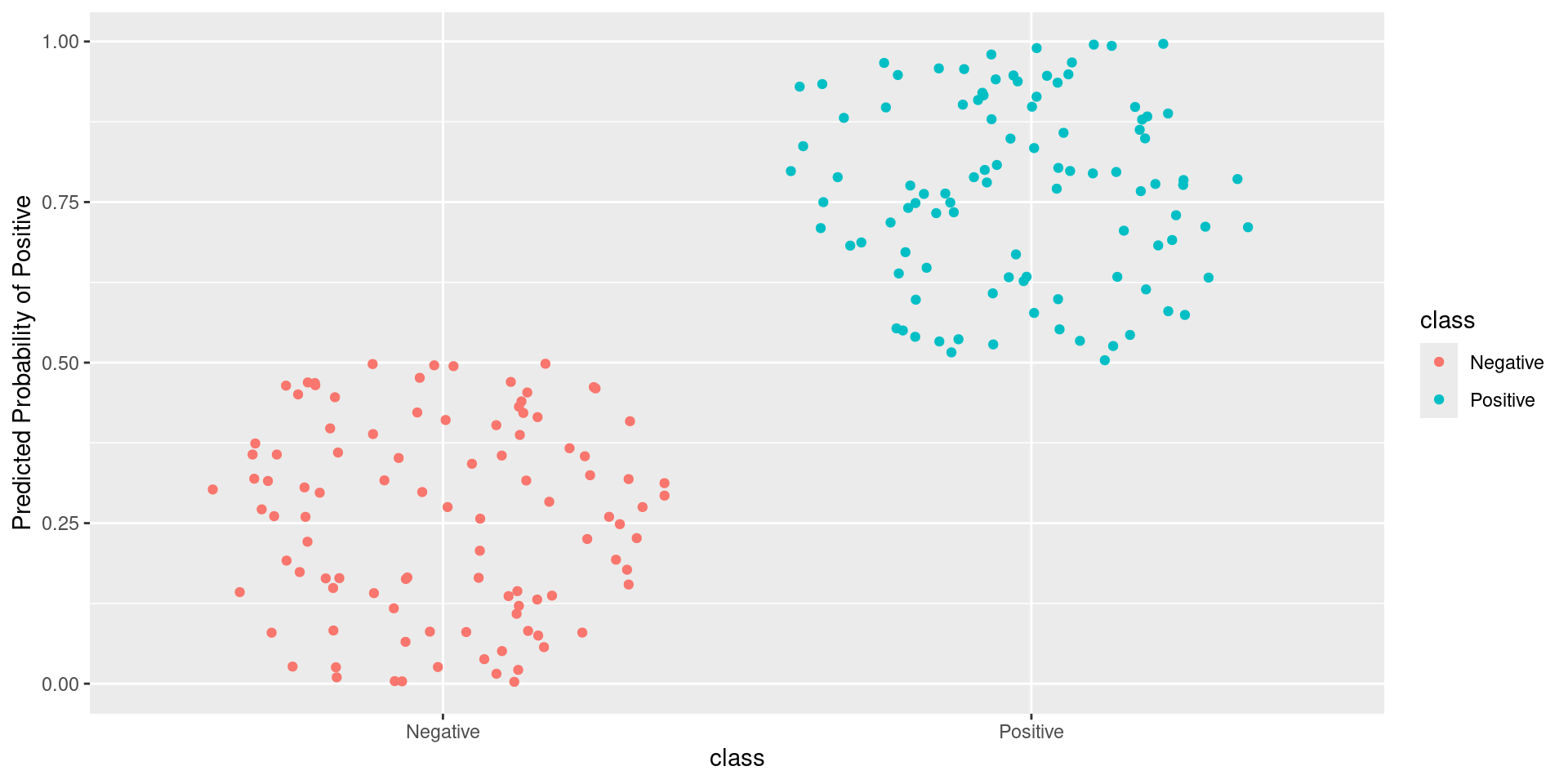
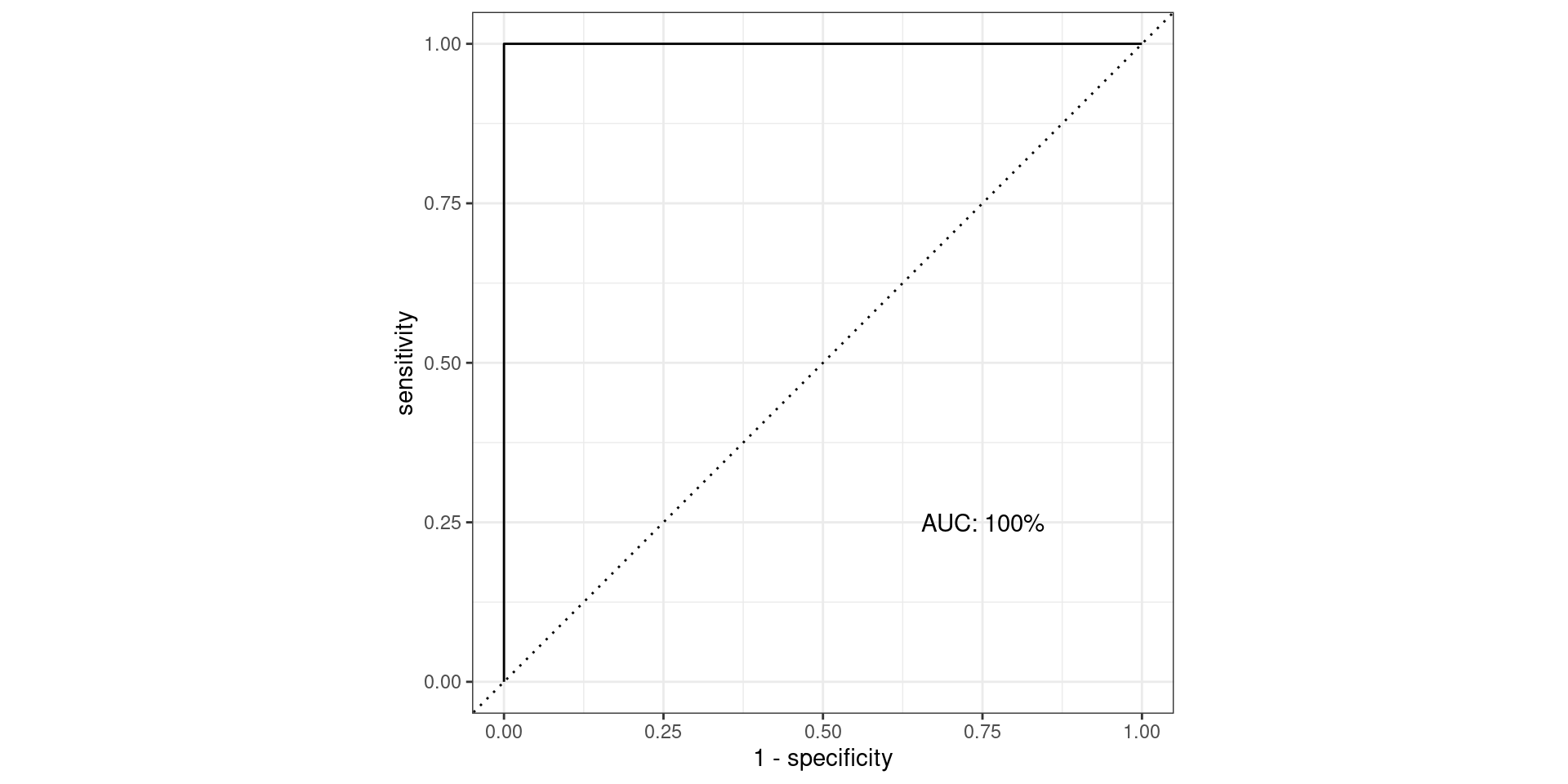
Pathological Example 3
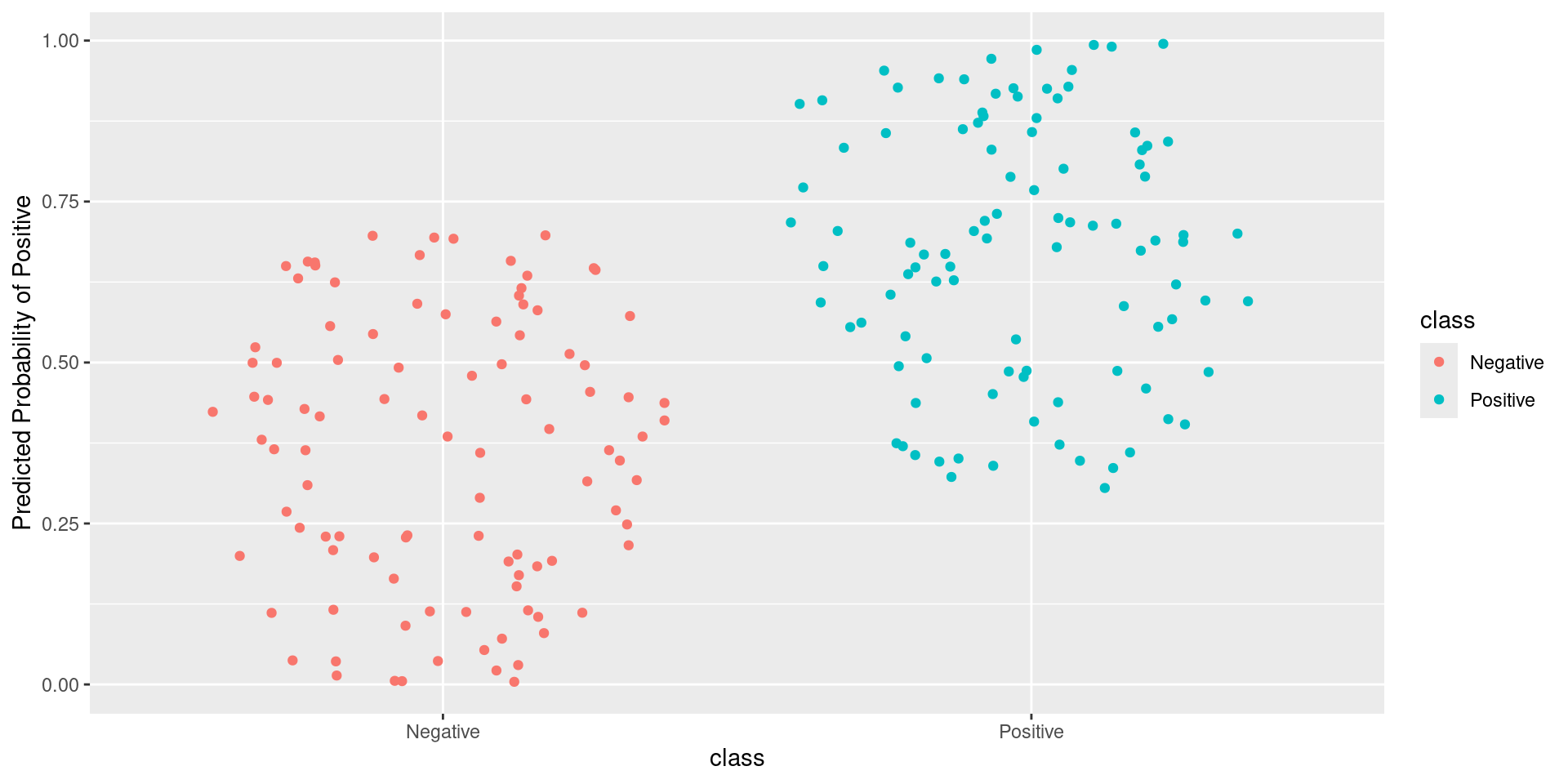
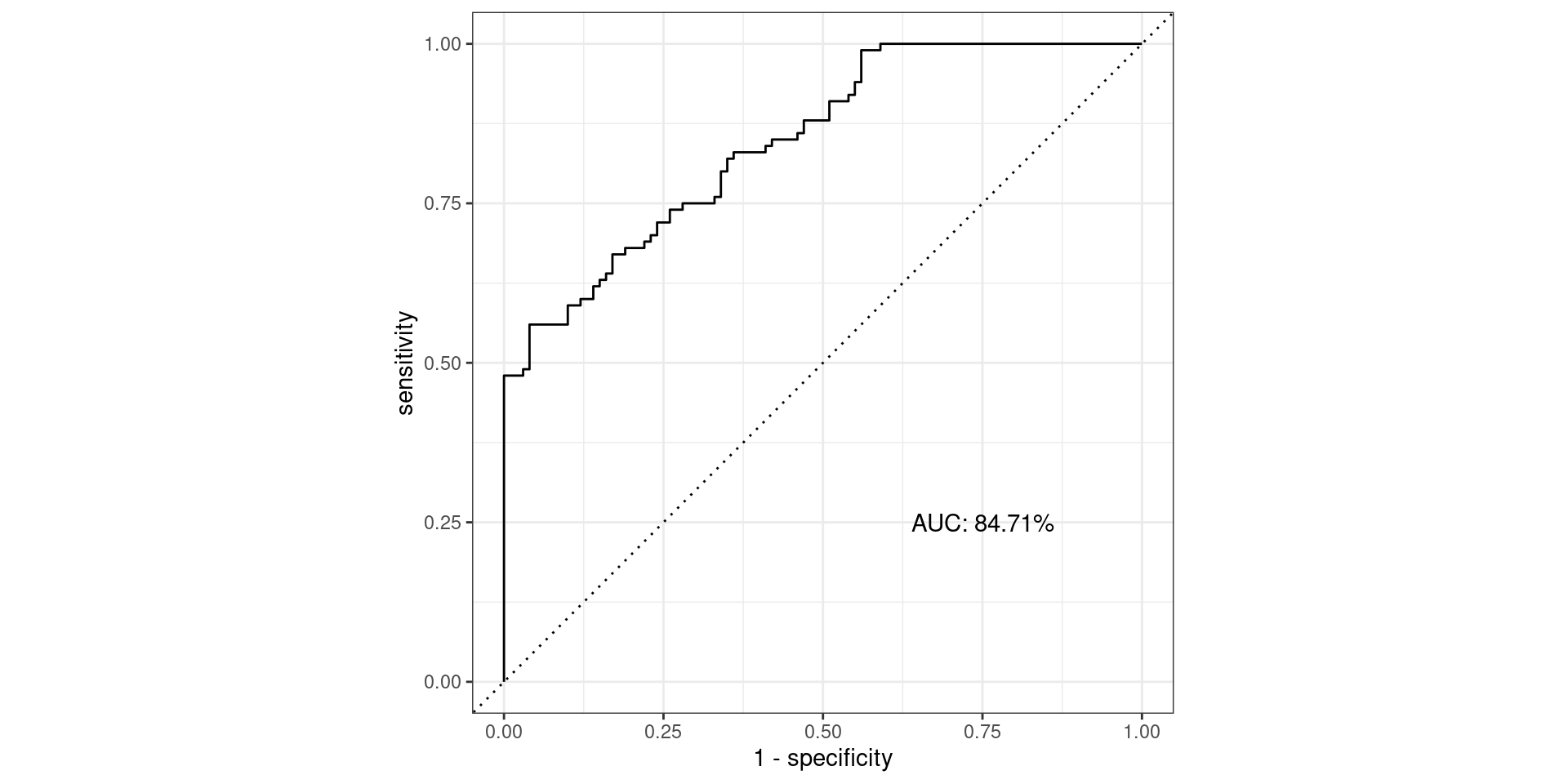
Pathological Example 3
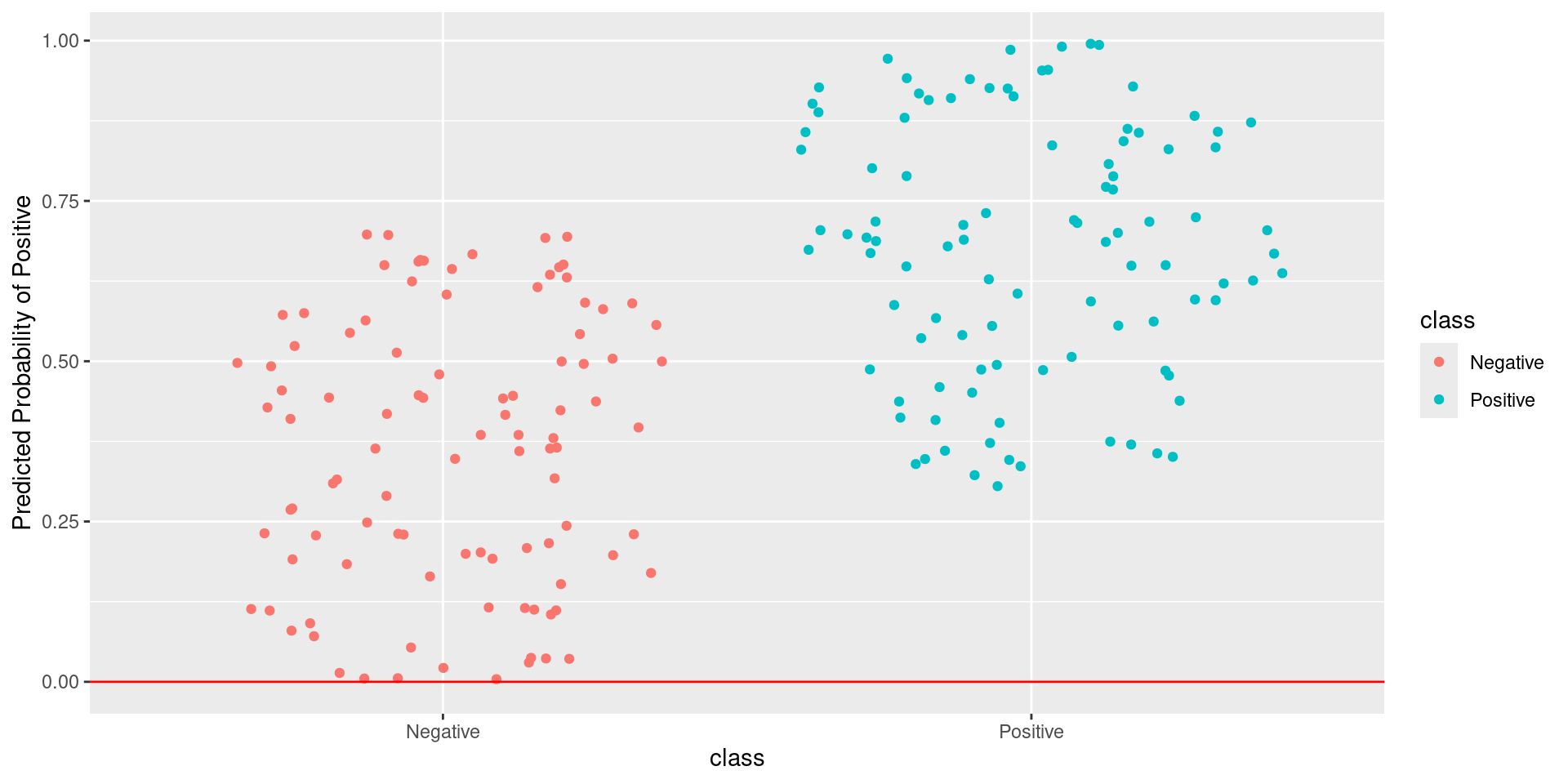
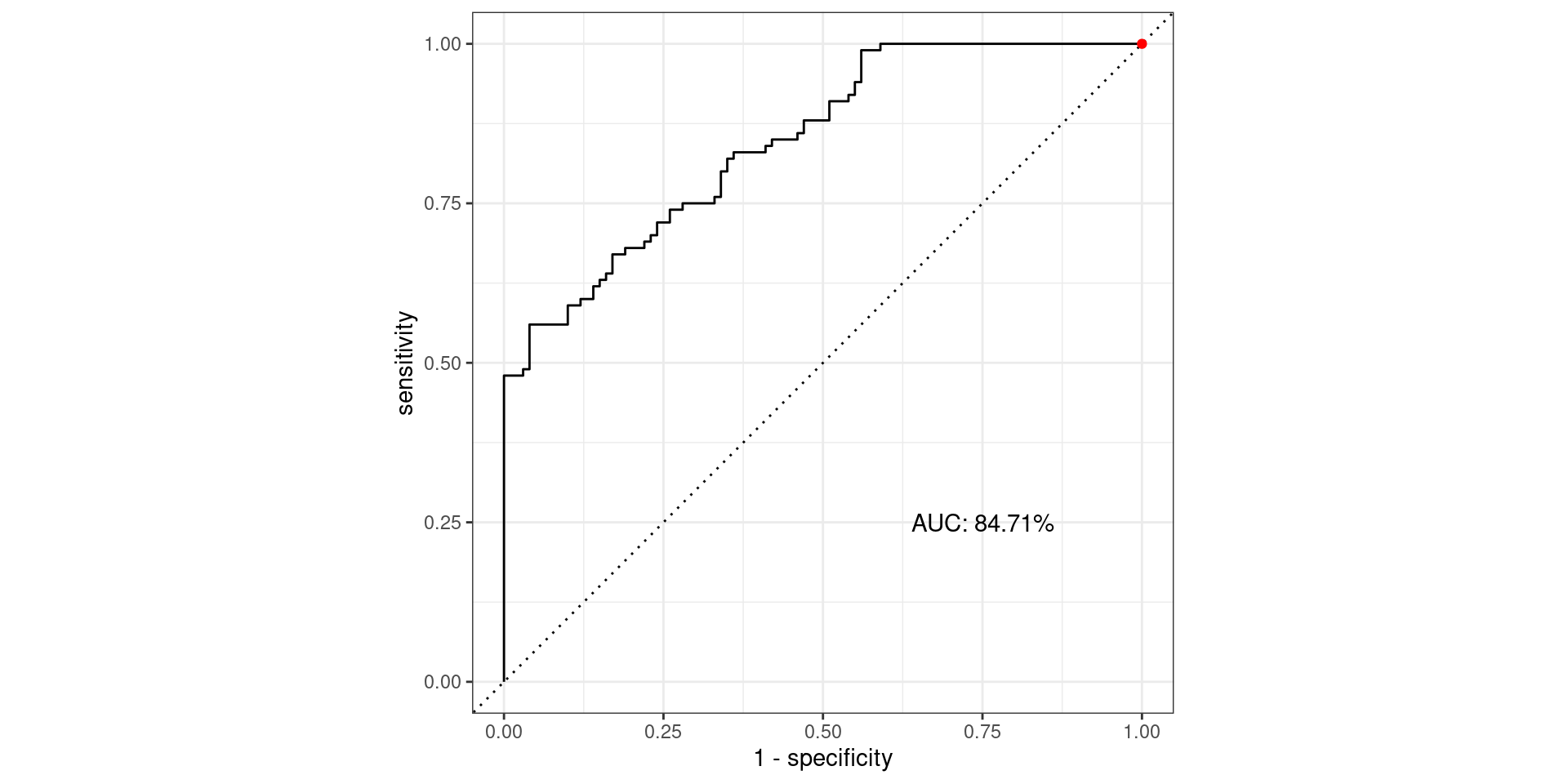
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{100}{100} = 1\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{100}{100} = 1\]
Pathological Example 3
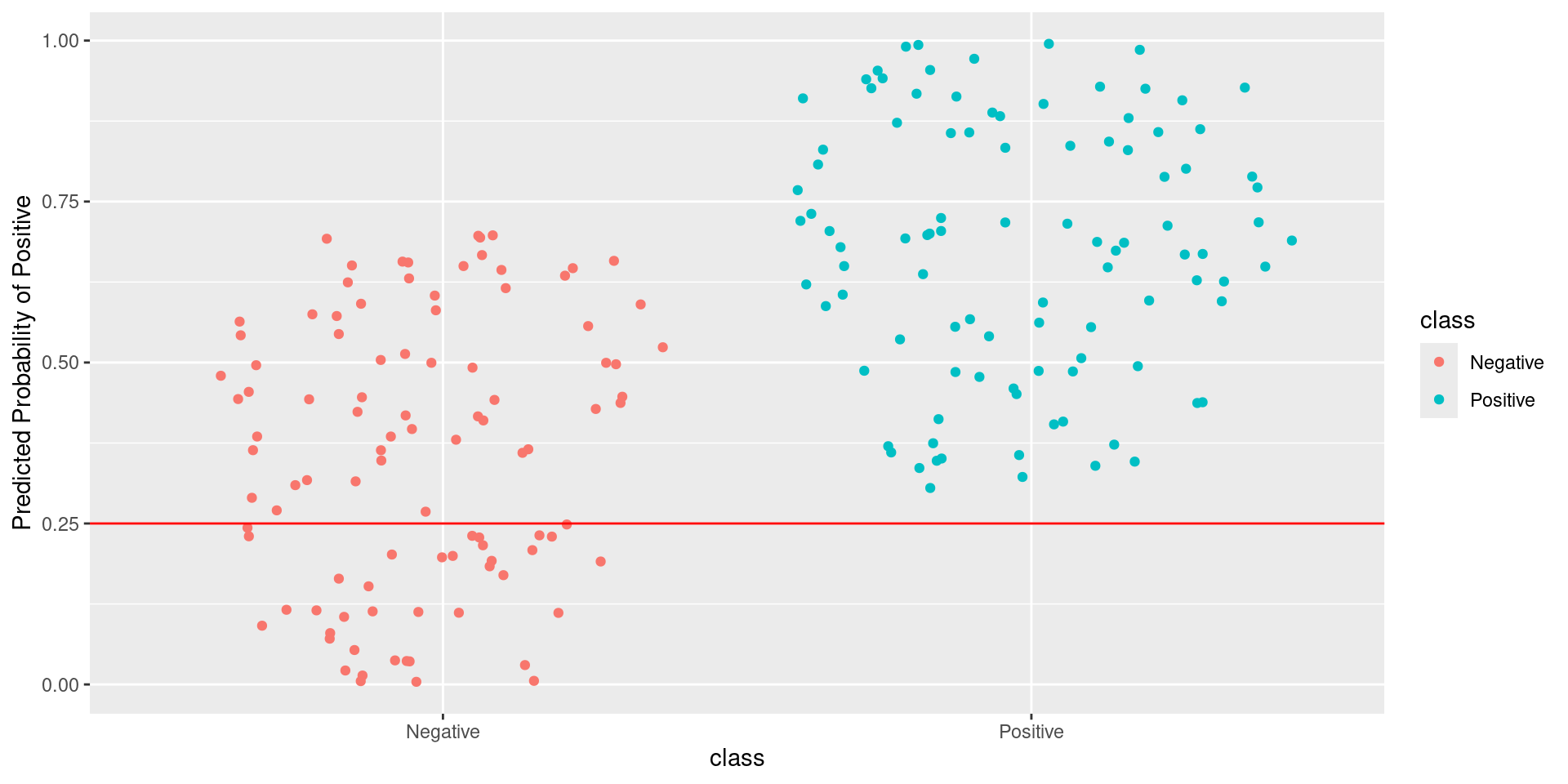
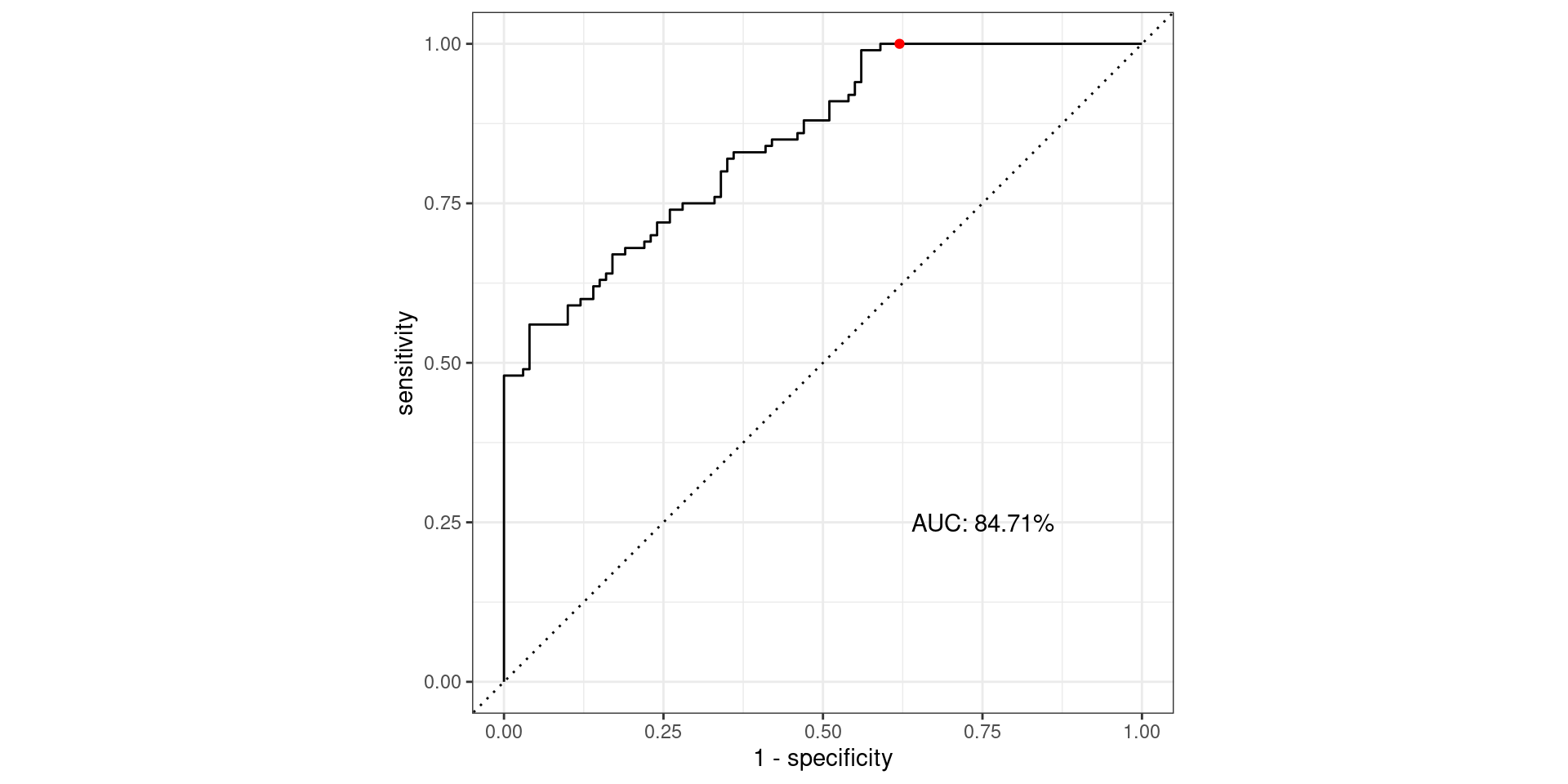
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{100}{100} = 1\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{62}{100} = 0.62\]
Pathological Example 3
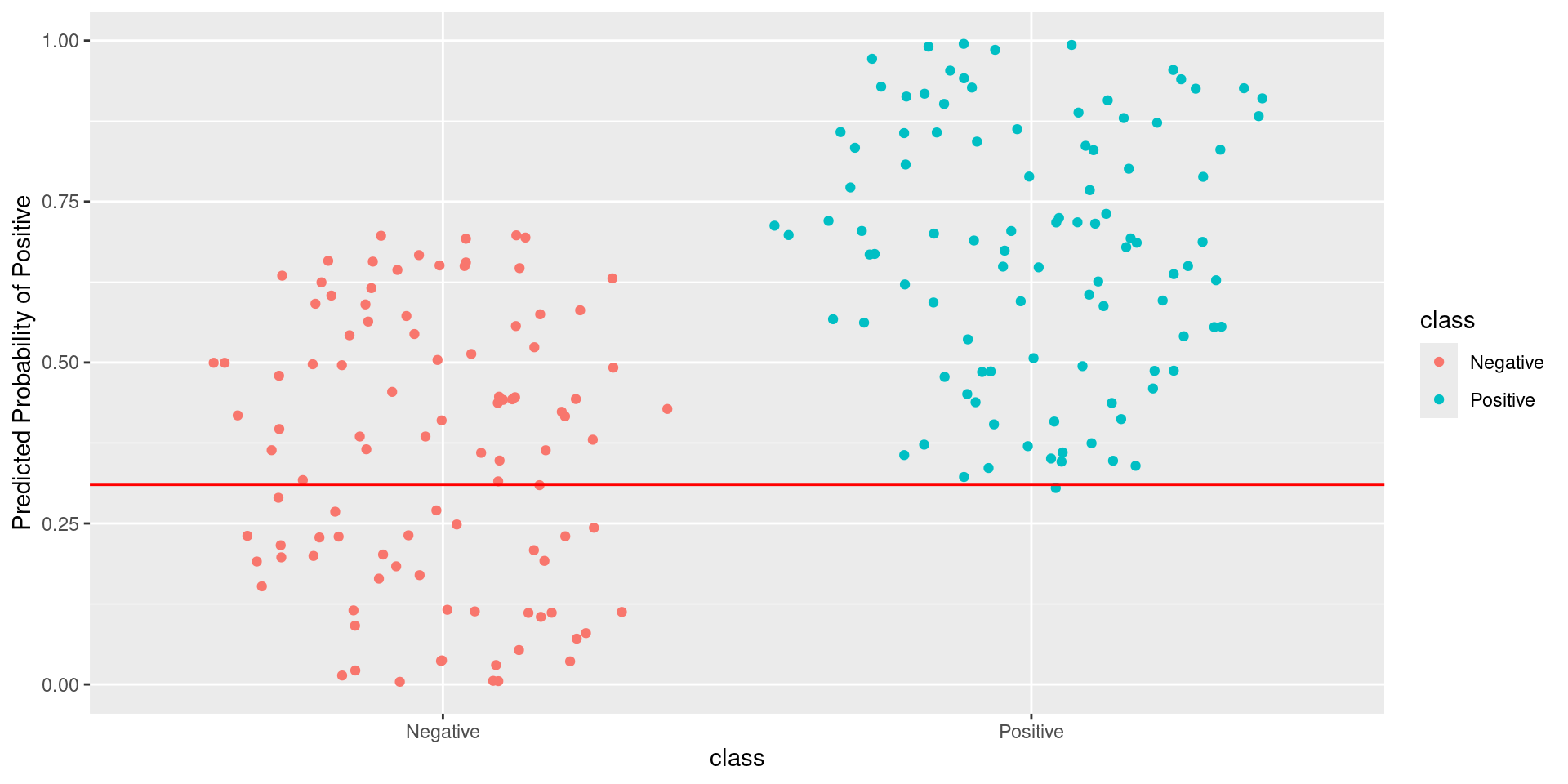
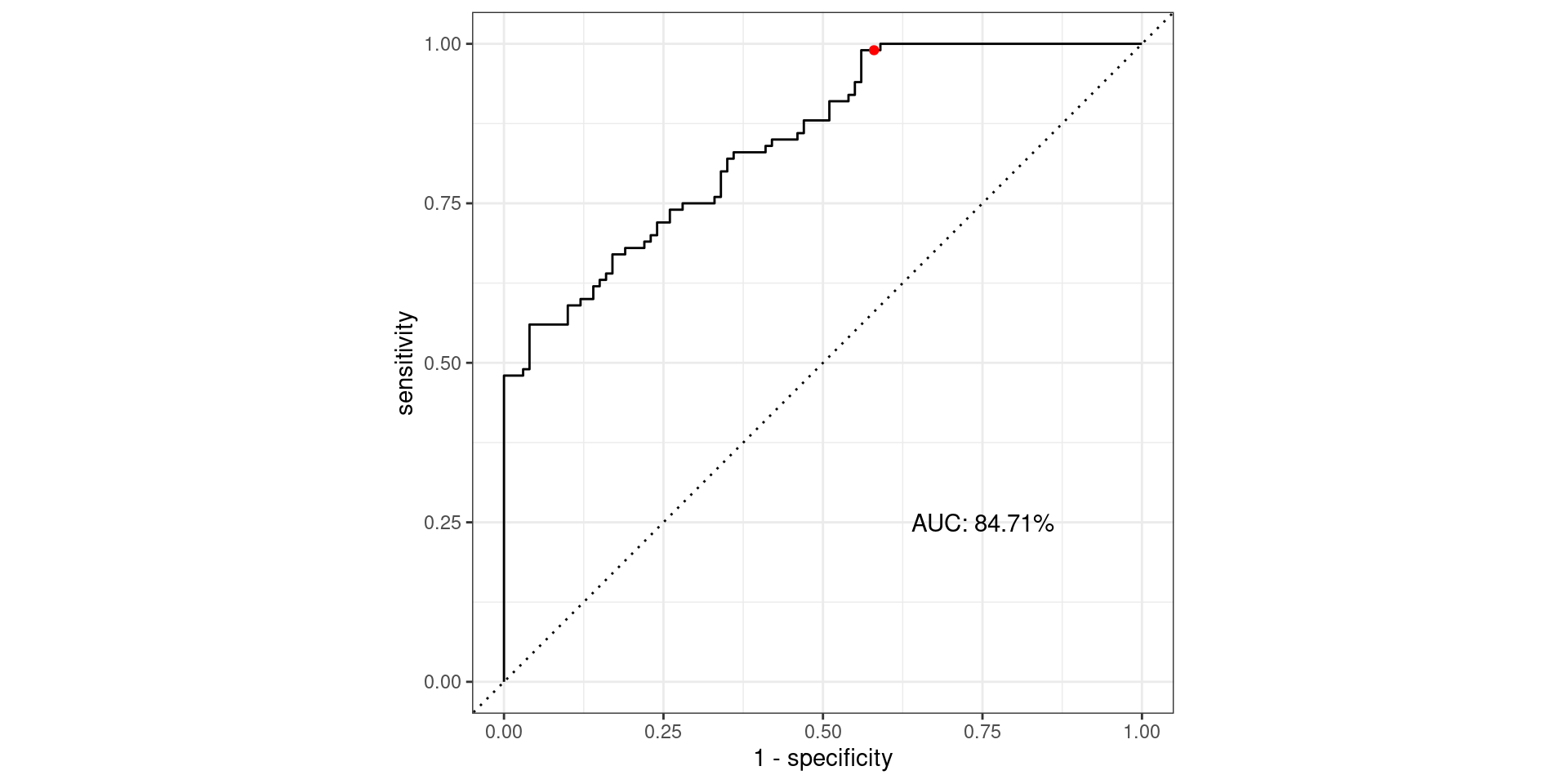
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{99}{100} = 0.99\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{58}{100} = 0.58\]
Pathological Example 3
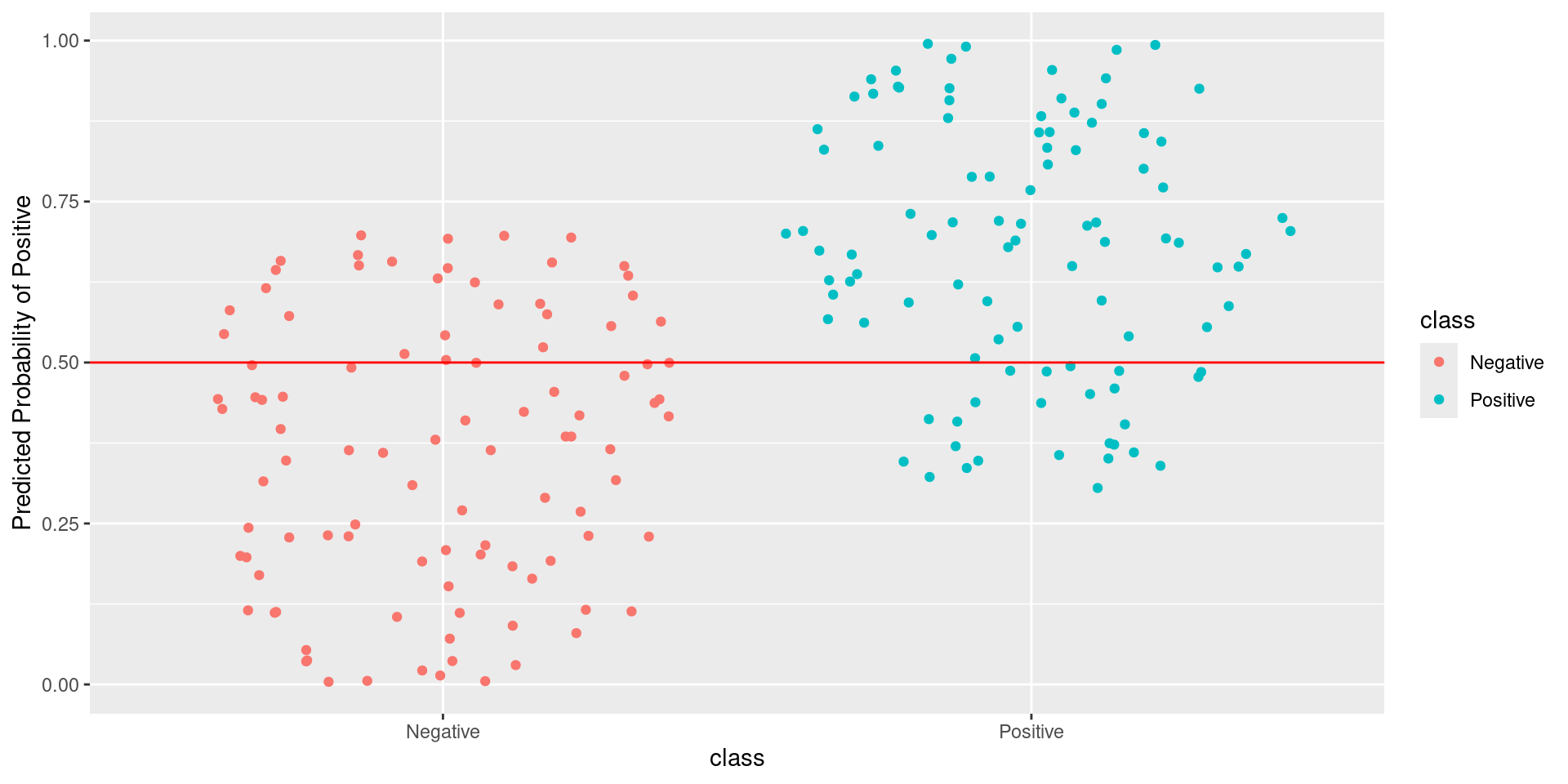
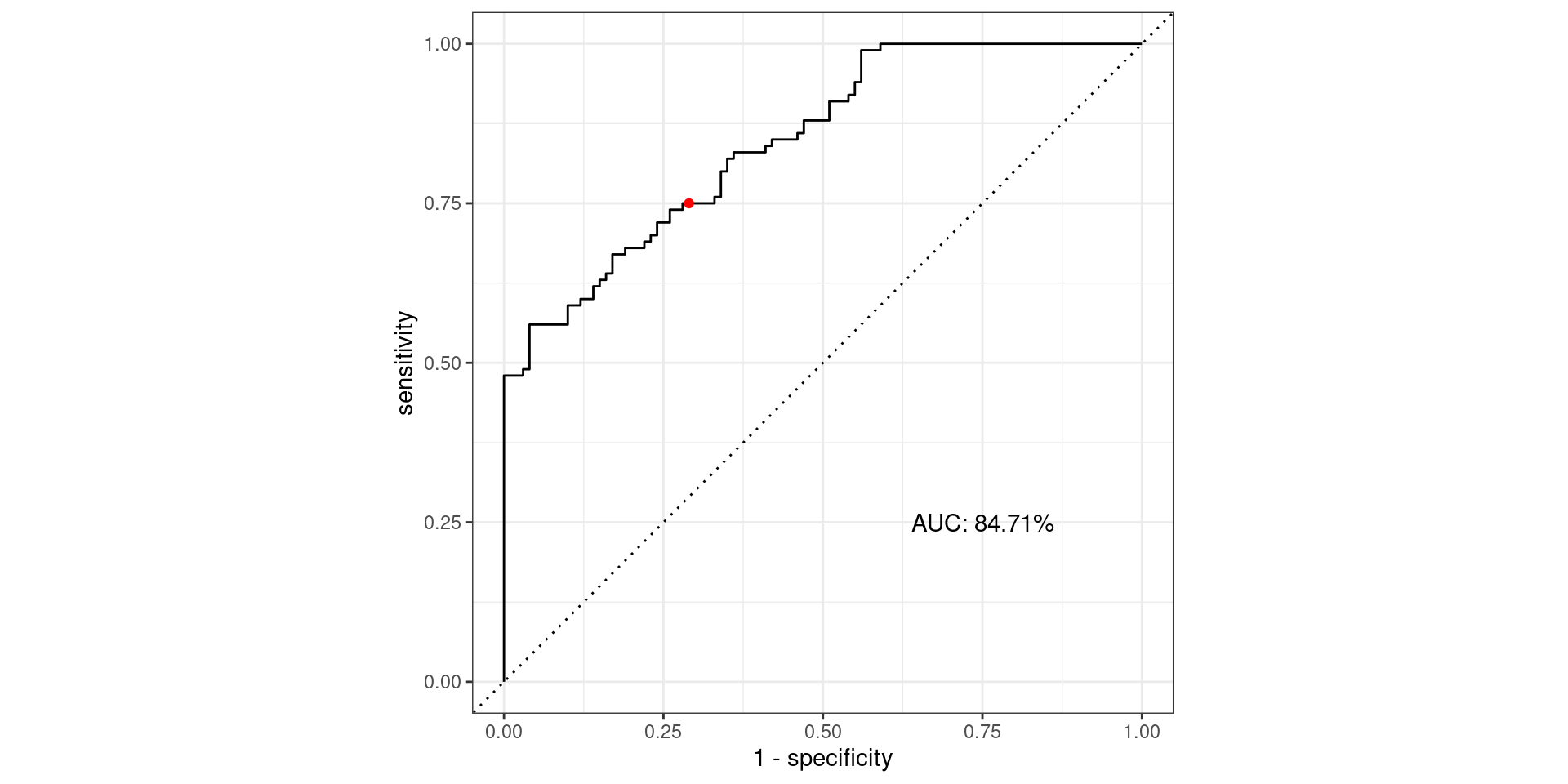
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{75}{100} = 0.75\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{29}{100} = 0.29\]
Pathological Example 3
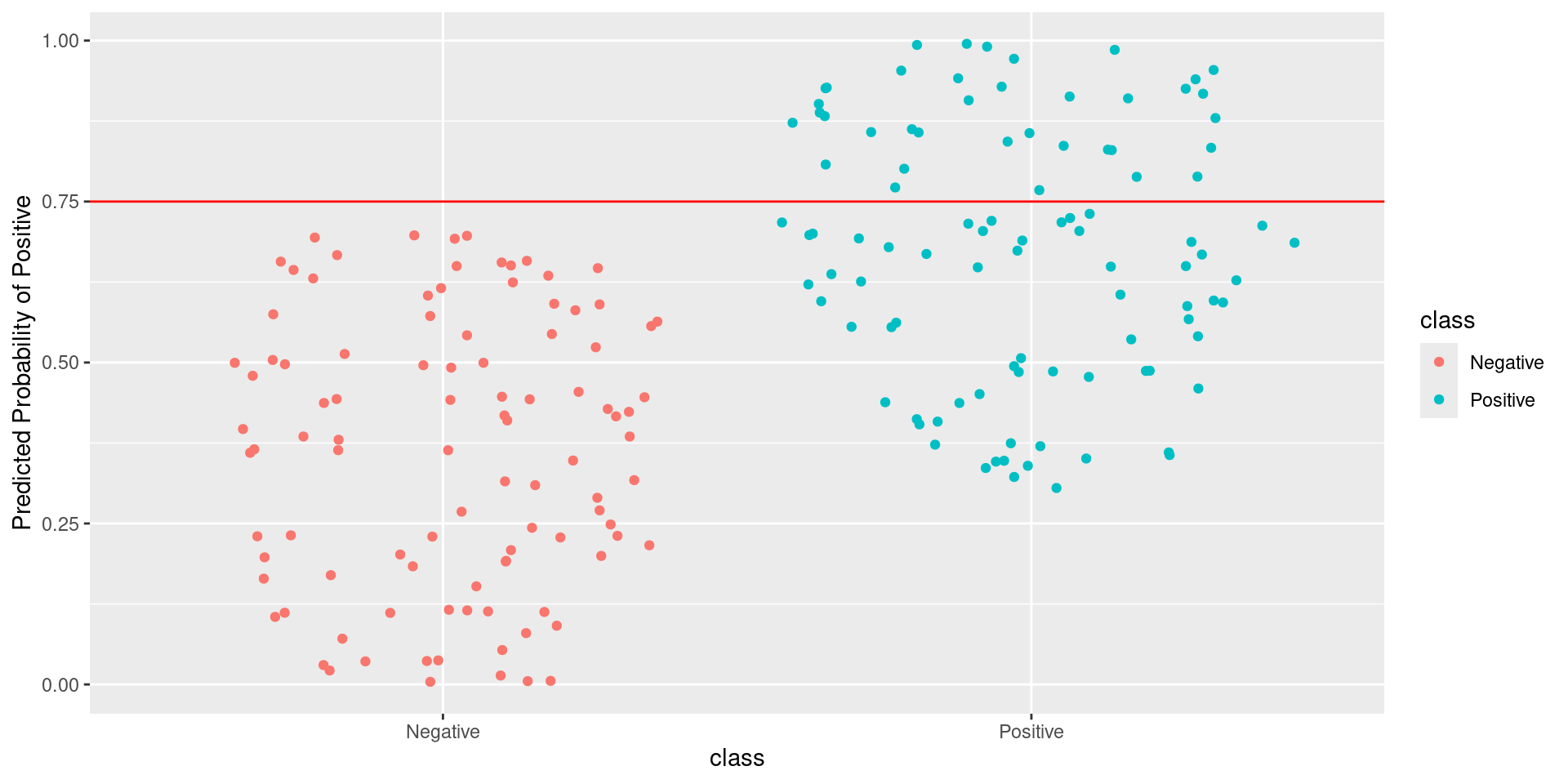
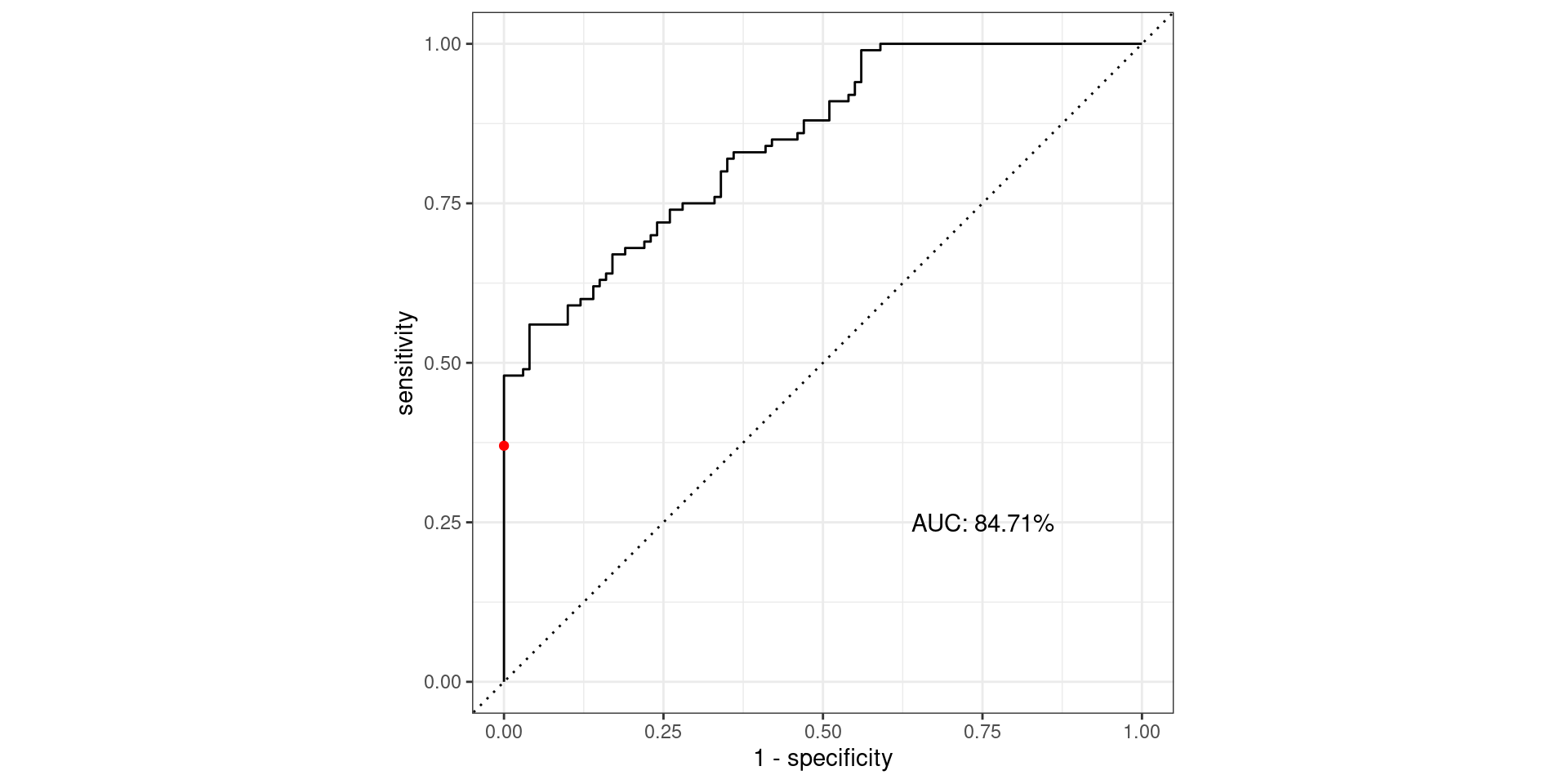
\[\text{Sensitivity} = \frac{TP}{TP + FN} = \frac{\text{Greens Above Line}}{\text{All Greens}} = \frac{37}{100} = 0.37\] \[1-\text{Specificity} = 1-\frac{TN}{TN + FP} = \frac{FP}{TN + FP} = \frac{\text{Reds Above Line}}{\text{All Reds}} = \frac{0}{100} = 0\]
Pathological Example 4
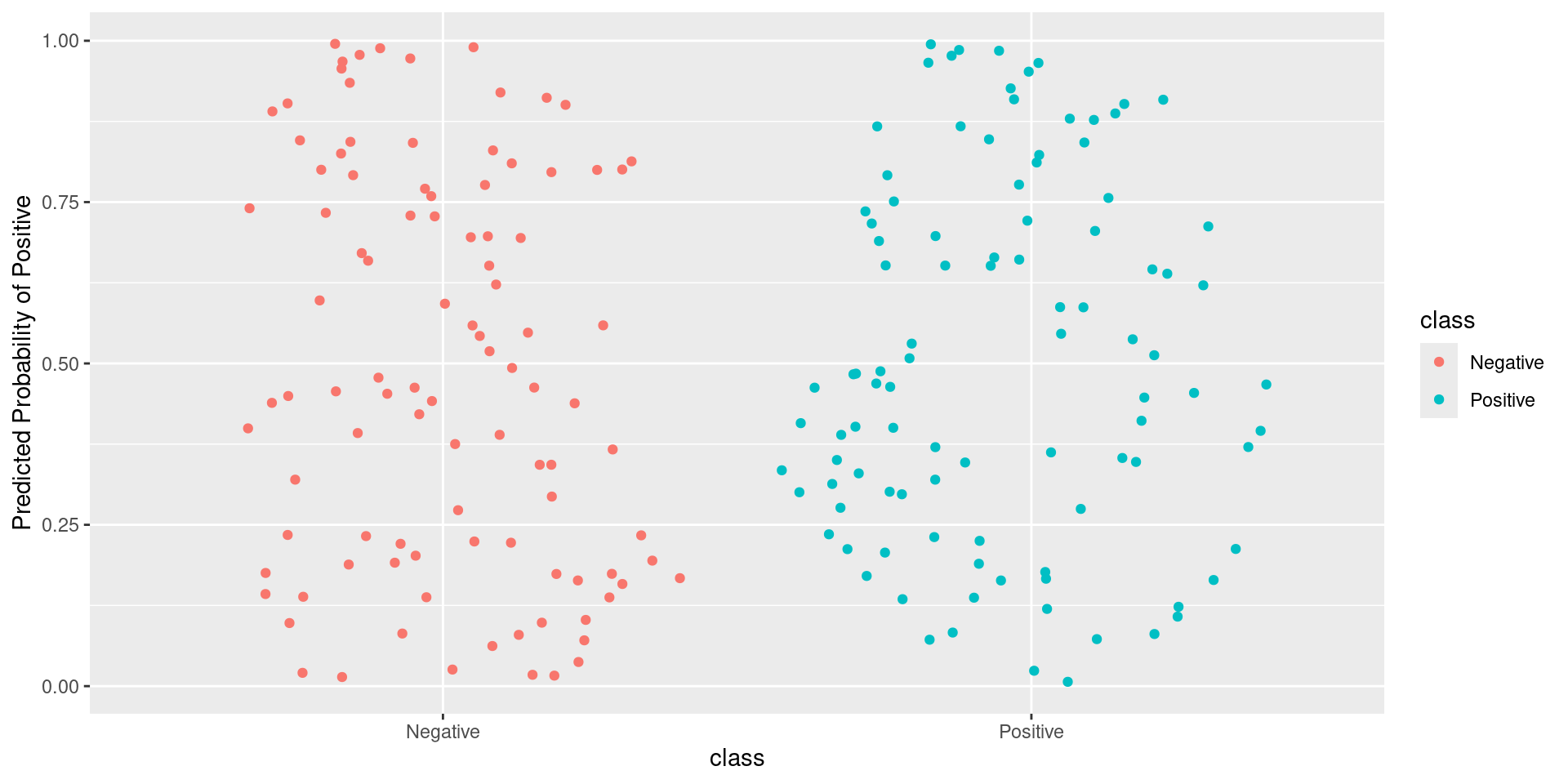
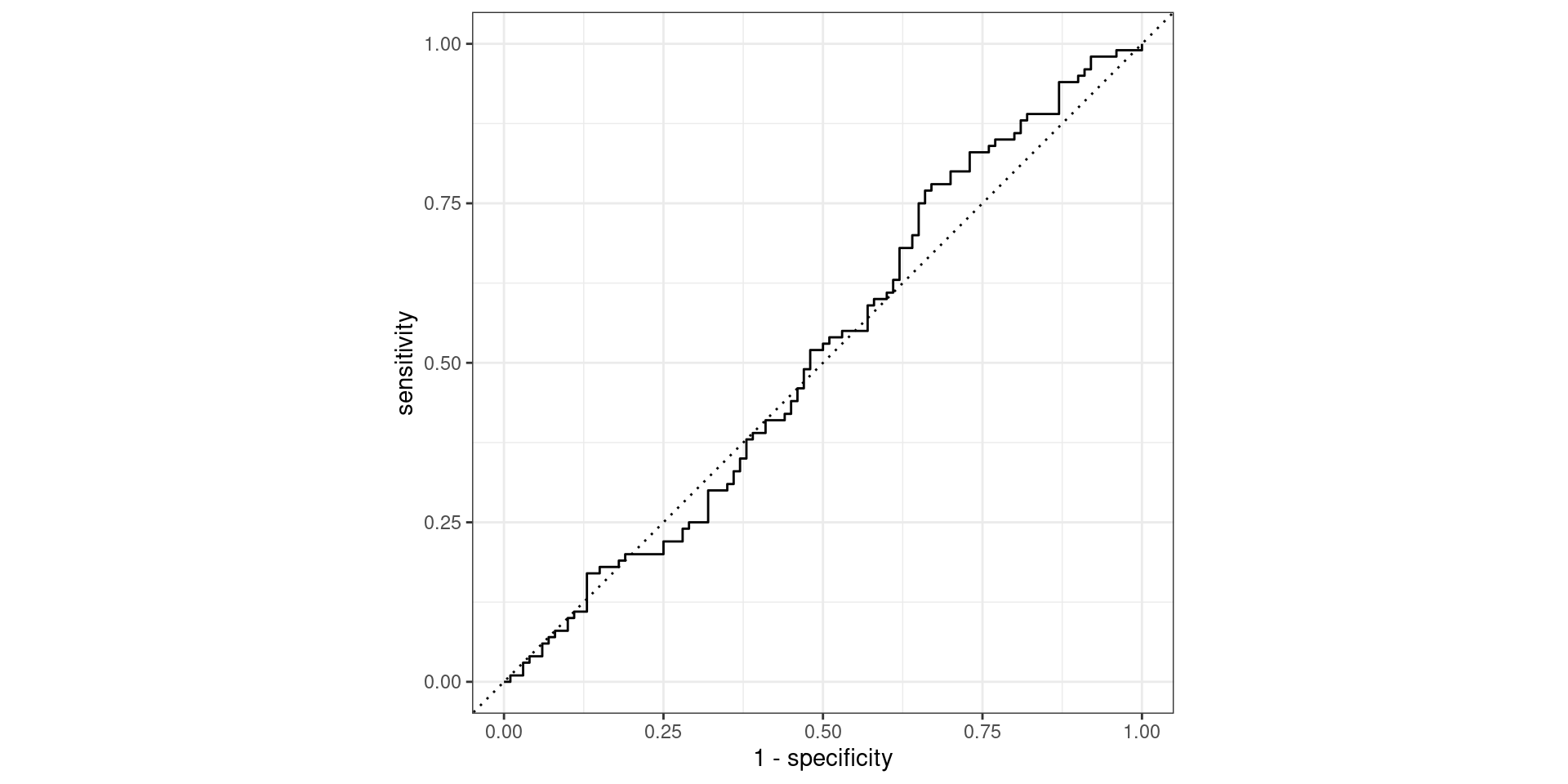
Pathological Example 5
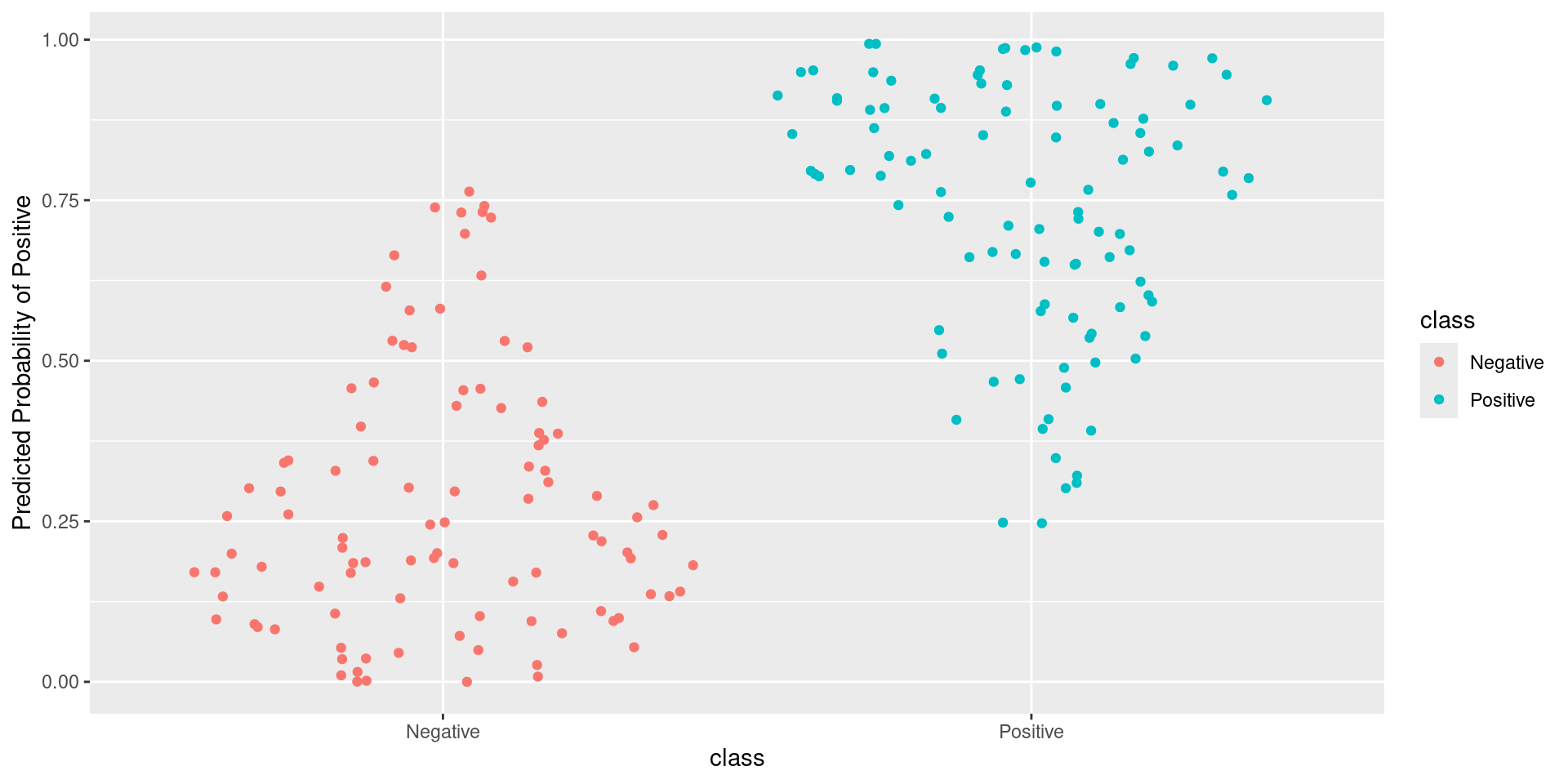
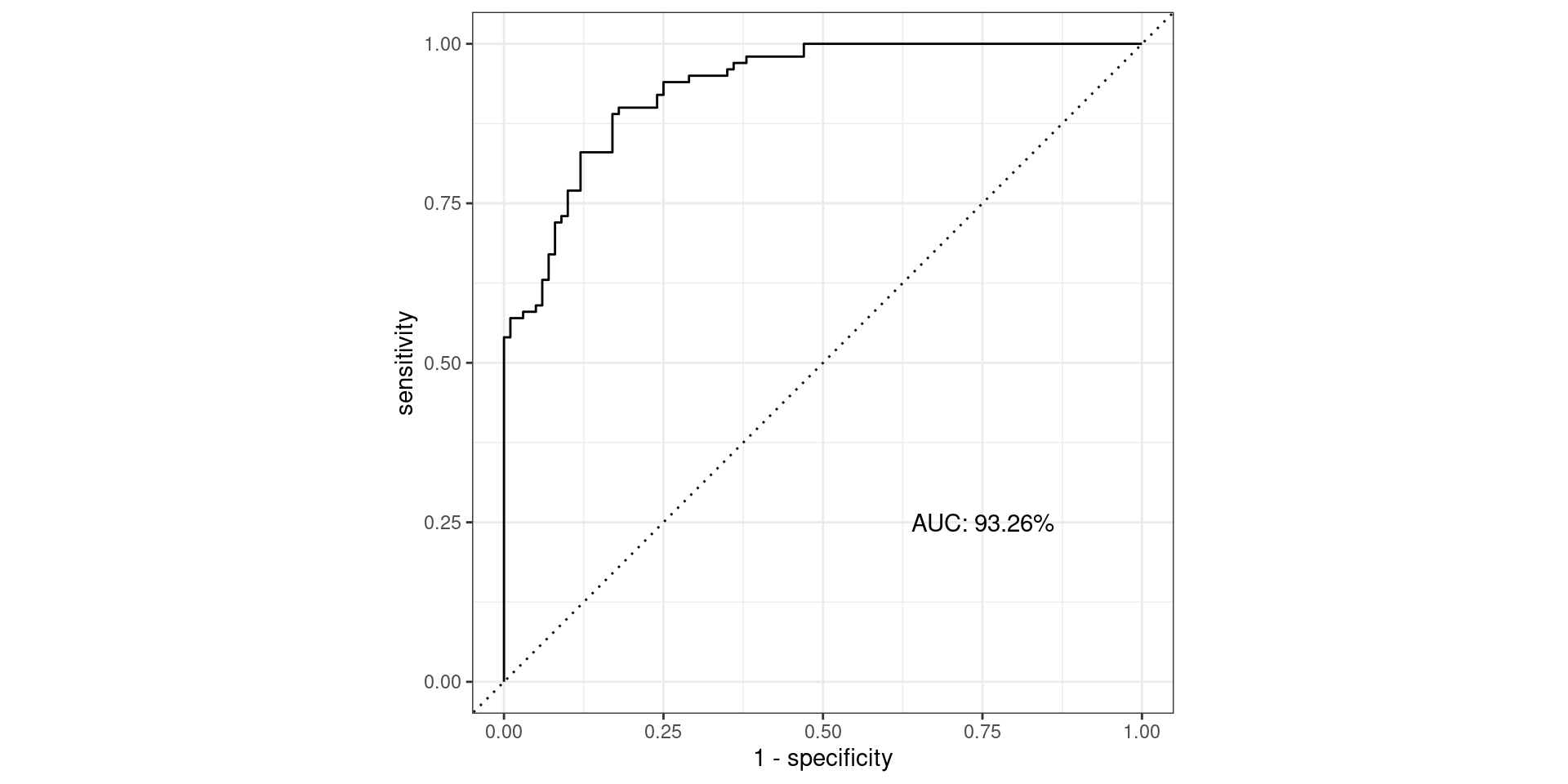
Pathological Example 6
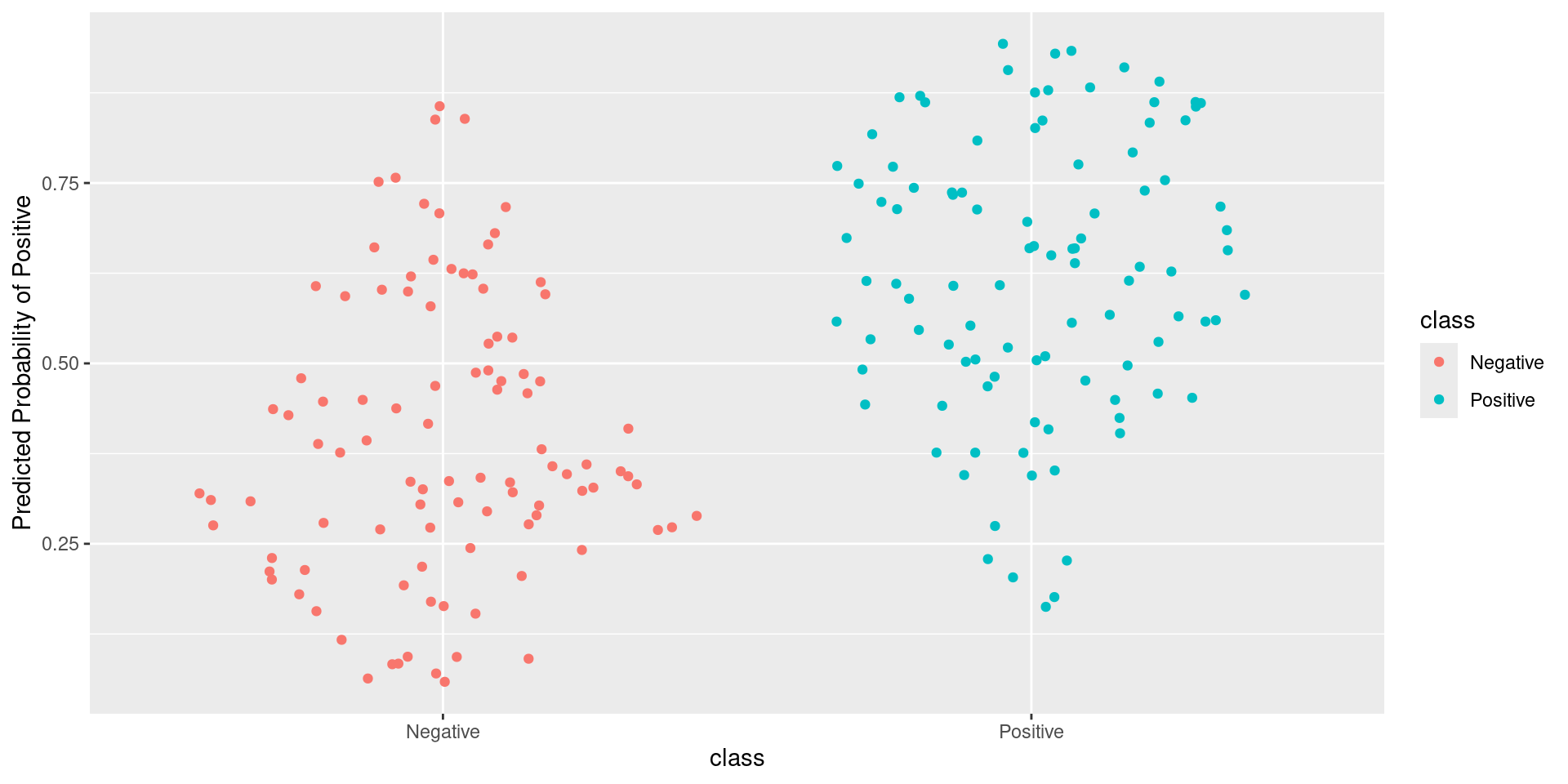
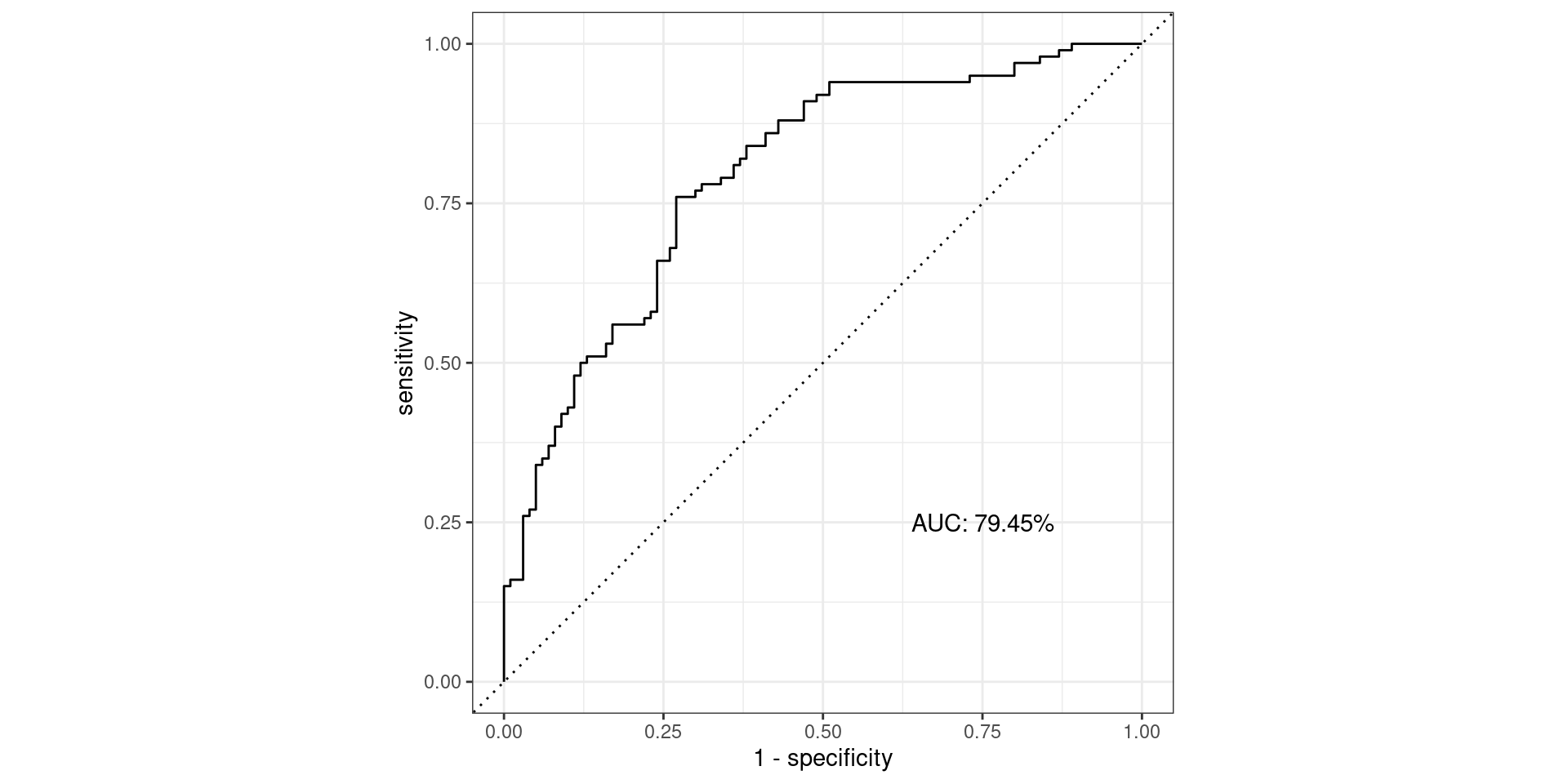
Pathological Example 7
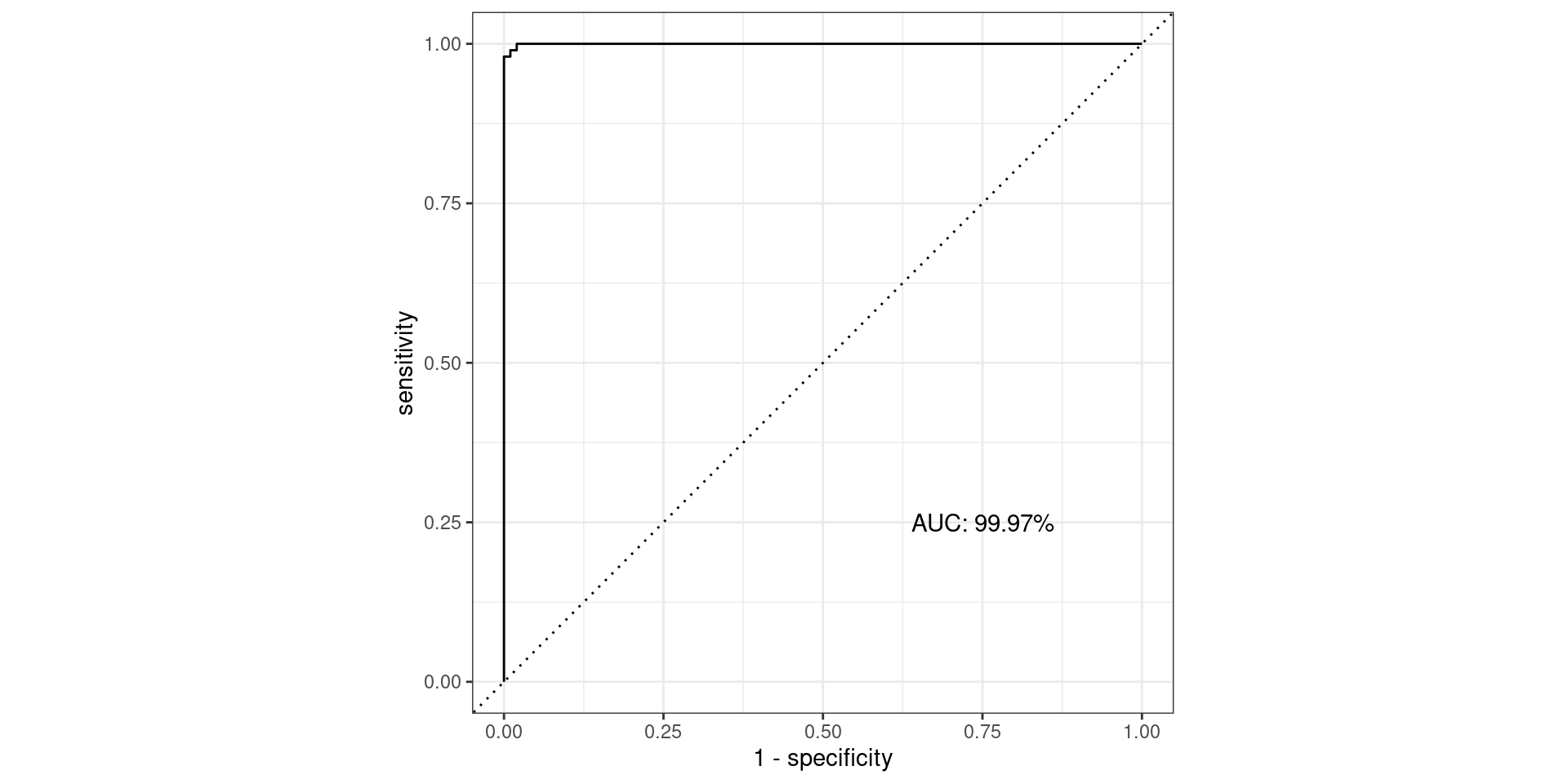
AUC Questions
- What should be the minimum AUC?
- What should be that maximum possible AUC?
Review of Classification Metrics
Review: Logistic Regression vs KNN
- Logistic regression \(\implies\) parametric , KNN \(\implies\) non-parametric.
- Logistic regression \(\implies\) only for classification problems (\(Y\) categorical), KNN \(\implies\) both regression and classification.
- Logistic regression is (more) interpretable, KNN is not.
- Logistic regression allows qualitative predictors. Euclidean distance with KNN does not allow for qualitative predictors.
- Prediction: KNN can be pretty good for small \(p\), that is, \(p \le 4\) and large \(n\). Performance of KNN deteriorates as \(p\) increases - curse of dimensionality.
Classification Metrics App
- Dr. F will split you into four groups
- On one of your computers connect to a tv and open this app
- Do the following based on your group number:
- 1: Choose plane on the first screen
- 2: Choose circle on the first screen
- 3: Choose parabola on the first screen
- 4: Choose sine curve on the first screen
- We will generate data from this population… do you think KNN or logistic regression will yield a better classifier? Why?
Classification Metrics App
- On the second tab generate a small test and training set
- On the third tab fit a KNN model with 5 neighbors and then a logistic regression model
- Which model do you think will perform better based on the plots you see?
- Choose the better model, click fit, and click on the fourth tab
Questions
Using the app, try and answer the following questions:
- Which of the metrics are most and least impacted by:
- Sample size
- Imbalanced data (i.e. proportion positive near 0 or 1)
- High noise
