MATH 427: Decision Trees
Eric Friedlander
Computational Set-Up
Tree-Based Methods
- Idea: stratify or segment the predictor space into simple regions
- Splitting rules used to segment the predictor space form a tree
- Can be used for both classification and regression
- Single tree called decision tree
- Simple and useful for interpretation
- Not the best in terms of prediction accuracy.
- Much more powerful: grow multiple trees and then combine their results
- bagging and boosting .
- Most powerful methods for tabular data are typically tree-based methods
Terminology for Trees
- Every split is considered to be a node
- First node at the top of the tree: root node (contains all the training data)
- Final nodes at the bottom of tree called leaves or terminal nodes
- Decision trees typically drawn with root at top and leaves at bottom
- Nodes in middle of tree called internal nodes
- The segments of the trees that connect nodes are known as branches
Terminology for Trees


Building a Tree
- Select predictor \(X_j\) and cut point \(s\) such that splitting the predictor space into the regions \(\{X|X_j < s\}\) and \(\{X|X_j \geq s\}\) leads to the greatest possible reduction in performance metric (e.g. SSE)
- For any \(j\) and \(s\), define \[R_1 = \{X|X_j < s\} \ \ \text{and} \ \ R_2 = \{X|X_j \geq s\}\]
- Find \(j\) and \(s\) that minimize \[SSE = \displaystyle \sum_{i \in R_1}\left(y_i - \hat{y}_{R_1}\right)^2 + \sum_{i \in R_2}\left(y_i - \hat{y}_{R_2}\right)^2\]
- Repeat process on each the two new regions
- Continue until a stopping criterion is reached
Prediction
- For new observation that falls in region \(R_j\):
- Regression: the mean response of the training set observations in \(R_j\)
- Classificaiton: majority vote response of the training set observations in \(R_j\)
Building a Tree and Prediction
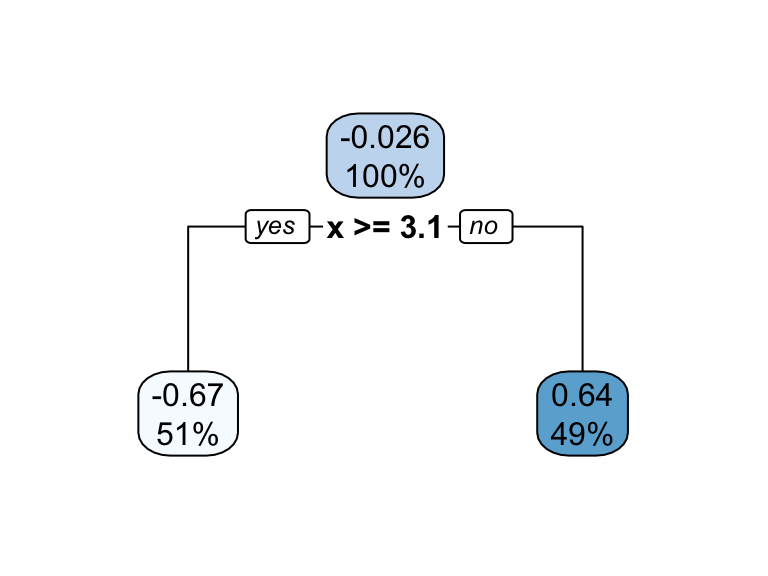
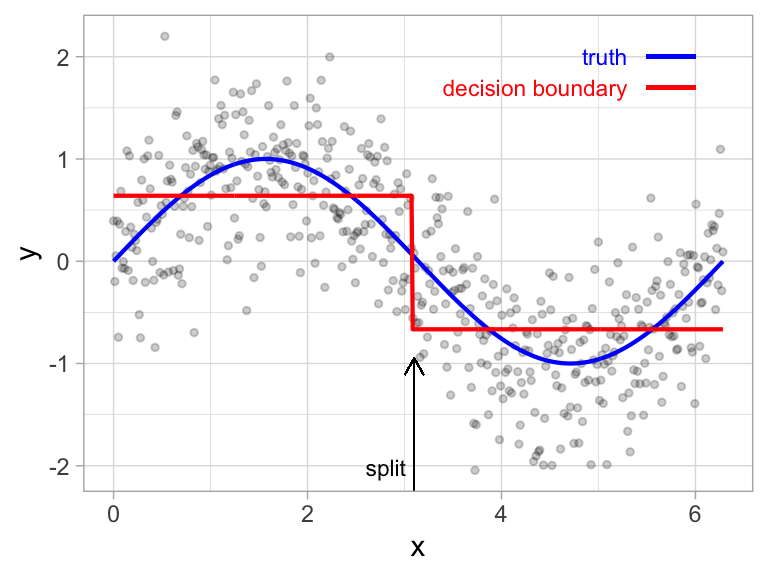
Building a Tree and Prediction


Building a Tree and Prediction

From ISLR
Building a Tree
- Anyone know what a greedy algorithm is?
- Computationally infeasible to consider every possible partition
- Idea: top-down, greedy approach known as recursive binary splitting.
- top-down because it begins at the top of the tree
- greedy because at each step of the tree-building process, the best split is made at that particular step, rather than looking ahead and picking a split that will lead to a better tree in some future step
- Important for determining whether to use a ordinal encoding or not
- Stop when each terminal node has fewer than some predetermined number of observations
Overfitting
- This process described above is likely to overfit the data
- One solution: require each split to improve performance by some amount
- Bad Idea: sometimes seemingly meaningless cuts early on enable really good cuts later on
- Good solution: pruning
- Build big tree and the prune off branches that are unnecessary
