MATH 427: Bagging and Boosting

Eric Friedlander

Computational Set-Up

library(tidyverse)
library(tidymodels)
library(rpart.plot)
library(knitr)
library(kableExtra)

tidymodels_prefer()

set.seed(427)

Ensemble Methods

  • Single regression or classification trees usually have poor predictive performance.
  • Ensemble Methods: use a collection of models (in this case, decision trees) to improve the predictive performance
    • Downside: Interpretability
  • Today:
    • Bagging
    • Random Forests
    • Boosting

Flexibility vs. Interpretability

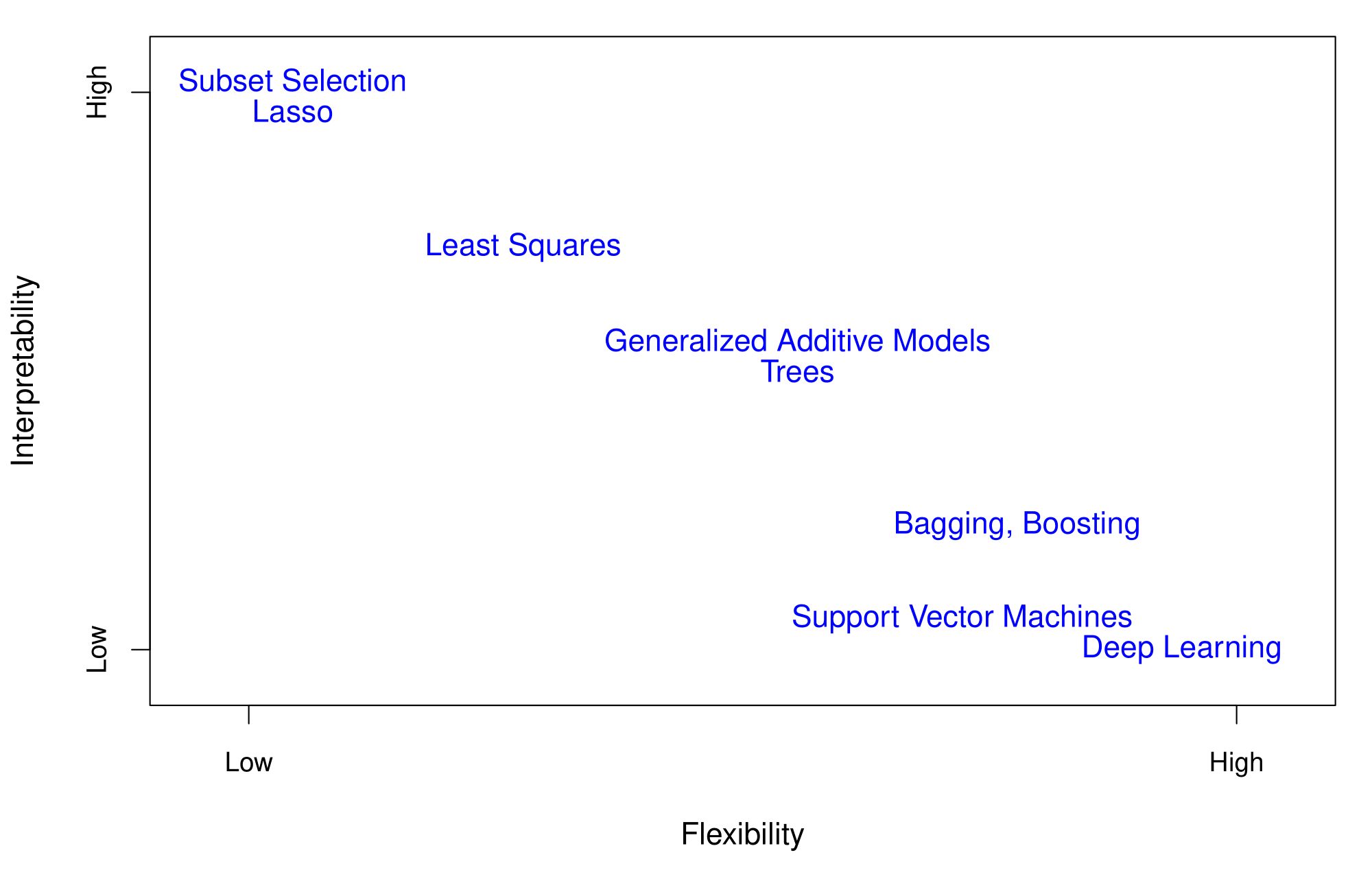
Adapted from ISLR, James et al.

Bagging

  • Bootstrap aggregation or bagging is a general-purpose procedure for reducing the variance of a statistical learning method.
  • Idea: Build multiple trees and average their results.
  • Result: Given a set of \(n\) independent observations (random variables) \(Z_1, \ldots, Z_n\), each with variance \(\sigma^2\), the variance of the mean/average \(\bar{Z} = \displaystyle \dfrac{Z_1 + Z_2 + \cdots + Z_n}{n}\) of the observations is \(\sigma^2/n\).
    • In other words, averaging a set of observations reduces variance.
  • In reality, we do not have multiple training datasets.

Bootstrapping

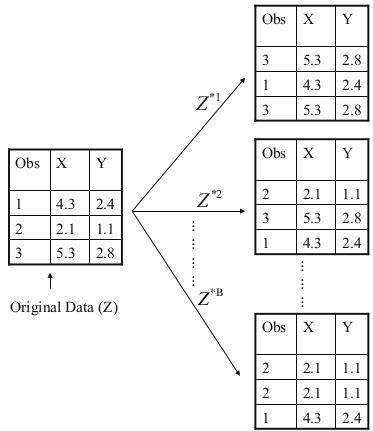
Adapted from ISLR, James et al.

Bagging

  • Take repeated bootstrap samples (say \(B\)) from the original dataset.
  • Build tree on each bootstrap sample and obtain predictions \(\hat{f}^{*b}(x), \ b=1, 2, \ldots, B\).
  • Average all the predictions: \[\hat{f}_{\text{bag}}(x) = \frac{1}{B}\sum_{i=1}^B\hat{f}^{*b}(x)\]
  • Trees not pruned: They have high variance, but low bias.
  • Classification: majority vote the overall prediction is the most commonly occurring class among the \(B\) predictions

Out-of-Bag Error Estimation

  • Bagging \(\Rightarrow\) fitting lots of models \(\Rightarrow\) computationally taxing
  • Bagging + Cross-validation \(\Rightarrow\) EXTREMELY COMPUTATIONALLY TAXING
  • On average, each bagged tree (constructed on each bootstrap sample) makes use of around two-thirds of the observations.
  • Remaining third observations referred to as out-of-bag (OOB) observations
  • For \(i^{th}\) observation, use the trees in which that observation was OOB. This will yield around \(B/3\) predictions for the \(i^{th}\) observation. Take their average to obtain a single prediction
  • Equivalent to LOOCV if \(B\) is large

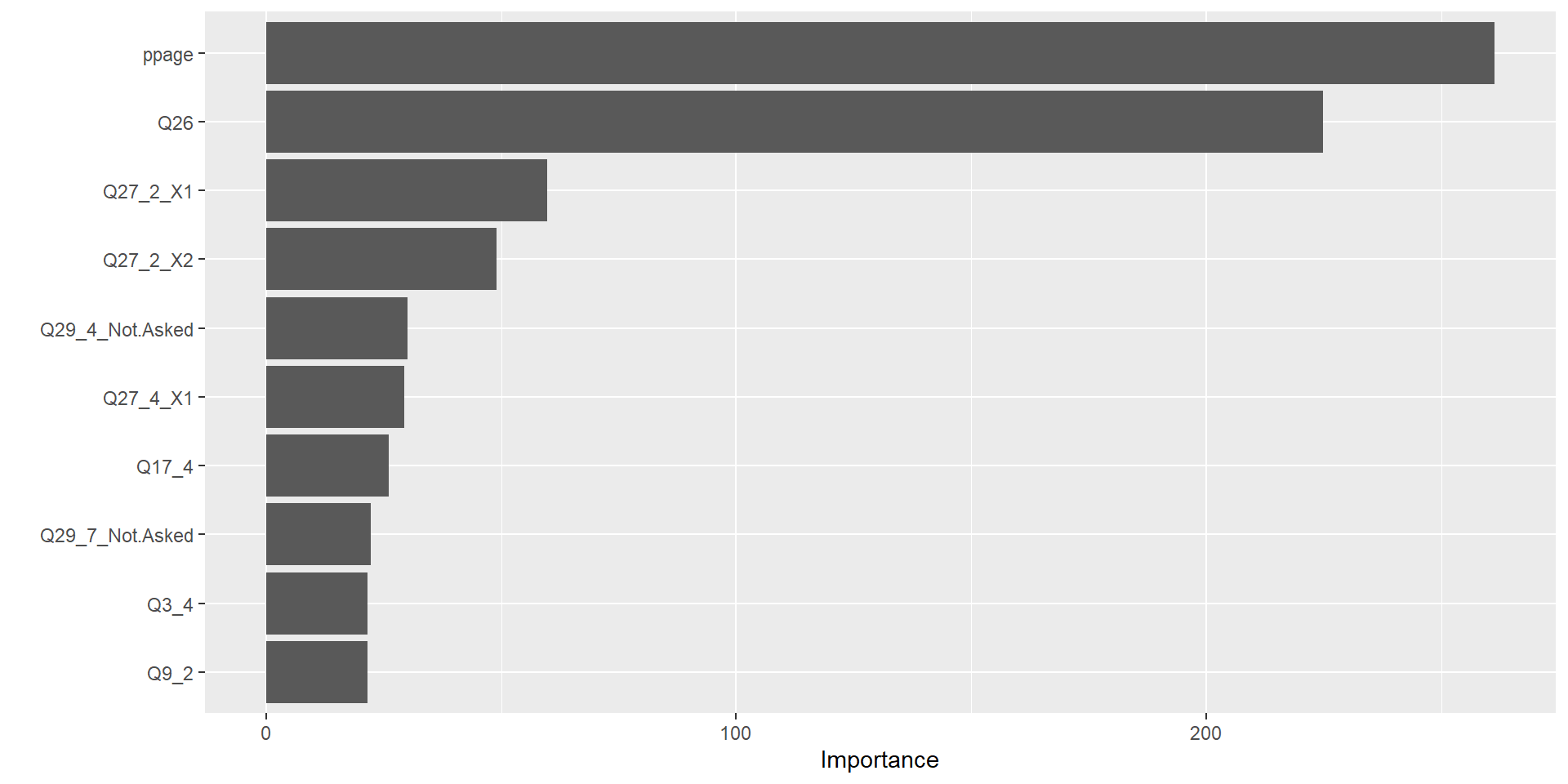
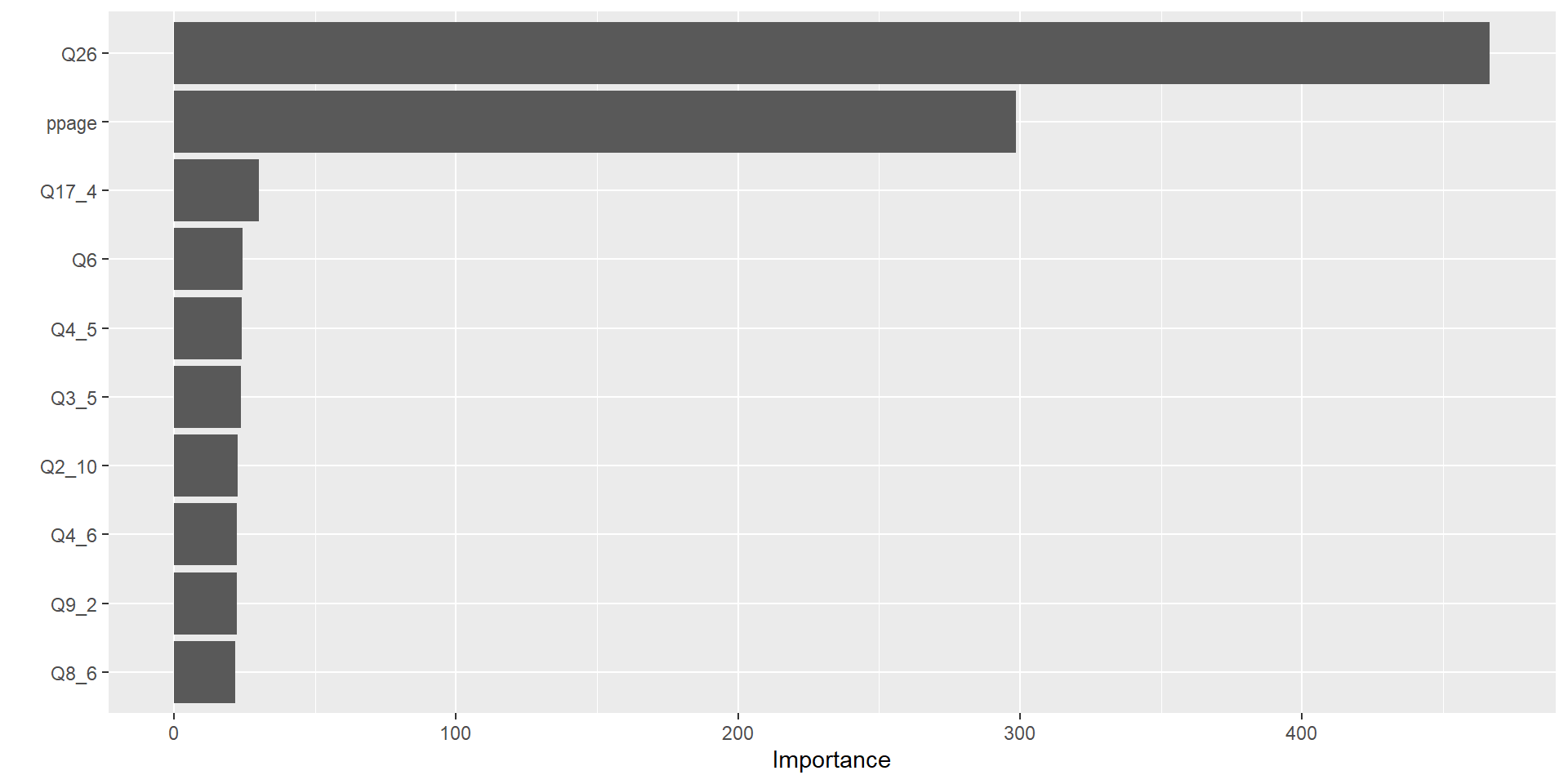
Variable Importance Measures

  • Bagging improves prediction accuracy at expense of interpretability
  • Can still obtain overall summary of importance of each predictor
    • Reduction in the loss function (e.g., SSE) attributed to each variable at each split is tabulated
    • A single variable could be used multiple times in a tree
    • Total reduction in the loss function across all splits by a variable are summed up and used as the total feature importance
    • A large value indicates an important predictor.

Bagging Implementation in R

Data: Voter Frequency

  • Info about data
  • Goal: Identify individuals who are unlikely to vote to help organization target “get out the vote” effort.
voter_data <- read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/non-voters/nonvoters_data.csv')

voter_clean <- voter_data |> 
  select(-RespId, -weight, -Q1) |>
  mutate(
    educ = factor(educ, levels = c("High school or less", "Some college", "College")),
    income_cat = factor(income_cat, levels = c("Less than $40k", "$40-75k ",
                                               "$75-125k", "$125k or more")),
    voter_category = factor(voter_category, levels = c("rarely/never", "sporadic", "always"))
  ) |> 
  filter(Q22 != 5 | is.na(Q22)) |> 
  mutate(Q22 = as_factor(Q22),
         Q22 = if_else(is.na(Q22), "Not Asked", Q22),
         across(Q28_1:Q28_8, ~if_else(.x == -1, 0, .x)),
         across(Q28_1:Q28_8, ~ as_factor(.x)),
         across(Q28_1:Q28_8, ~if_else(is.na(.x) , "Not Asked", .x)),
         across(Q29_1:Q29_10, ~if_else(.x == -1, 0, .x)),
         across(Q29_1:Q29_10, ~ as_factor(.x)),
         across(Q29_1:Q29_8, ~if_else(is.na(.x) , "Not Asked", .x)),
        Party_ID = as_factor(case_when(
          Q31 == 1 ~ "Strong Republican",
          Q31 == 2 ~ "Republican",
          Q32 == 1  ~ "Strong Democrat",
          Q32 == 2 ~ "Democrat",
          Q33 == 1 ~ "Lean Republican",
          Q33 == 2 ~ "Lean Democrat",
          TRUE ~ "Other"
        )),
        Party_ID = factor(Party_ID, levels =c("Strong Republican", "Republican", "Lean Republican",
                                                "Other", "Lean Democrat", "Democrat", "Strong Democrat")),
        across(!ppage, ~as_factor(if_else(.x == -1, NA, .x))))

Split Data

set.seed(427)

voter_splits <- initial_split(voter_clean, prop = 0.7, strata = voter_category)
voter_train <- training(voter_splits)
voter_test <- testing(voter_splits)

Define Model

  • trees: kind of a tuning parameter… want to select value that is large enough but doesn’t matter past that
bagged_model <- rand_forest(trees = 500, mtry = .cols()) |> 
  set_engine("ranger", importance = "impurity") |> 
  set_mode("classification")

Define Recipe

bag_recipe <- recipe(voter_category ~ . , data = voter_train) |> 
  step_indicate_na(all_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_integer(educ, income_cat, Party_ID, Q2_2:Q4_6, Q6, Q8_1:Q9_4, Q14:Q17_4,
               Q25:Q26) |> 
  step_impute_median(all_numeric_predictors()) |> 
  step_impute_mode(all_nominal_predictors()) |> 
  step_dummy(all_nominal_predictors(), one_hot = TRUE)

Define Workflow and Fit

# need to install ranger
bag_wf <- workflow() |> 
  add_model(bagged_model) |> 
  add_recipe(bag_recipe)

bagged_fit <- bag_wf |> 
  fit(voter_train)

Evaluate performance

augment(bagged_fit, new_data = voter_test) |> 
  accuracy(truth = voter_category, estimate = .pred_class)
# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy multiclass     0.648

Variable Importance

library(vip)
vip(bagged_fit)

Bagging: Disadvantages

  • improves prediction performance but reduces interpretability
  • trees in bagging not completely independent of each other since all the original features are considered at every split of every tree
  • tree correlation: trees from different bootstrap samples typically have similar structure to each other (especially at the top of the tree)
    • prevents bagging from further reducing the variance of the individual models
  • Random forests extend and improve upon bagged decision trees by reducing this correlation and thereby improving the accuracy of the overall ensemble.

Bagging: Disadvantages

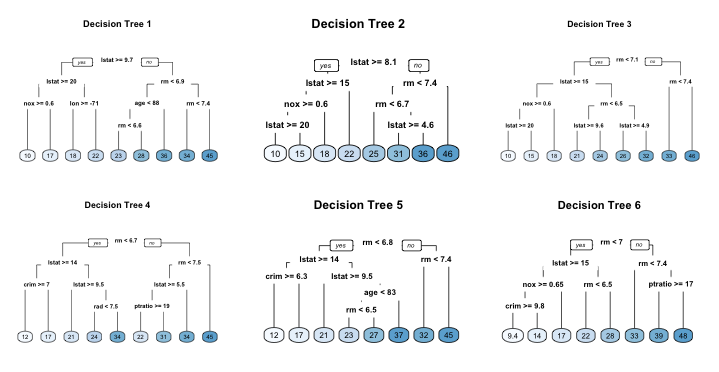
Adapted from Hands-On Machine Learning, Boehmke & Greenwell

Random Forests

Random Forests

  • De-correlates bagged trees \(\Rightarrow\) reducing variance
  • As in bagging, we build a number of decision trees on bootstrapped training samples.
  • Algorithm: do the following to build each tree
    • Generate bootstrapped sample of training data
    • Randomly select \(m\) predictors
    • Pick best variable/split-oint from these \(m\)
    • Split node into two child nodes
    • Stop when typical stopped criteria is hit (not pruning)
  • Note: A fresh sample of \(m\) predictors is taken at each split
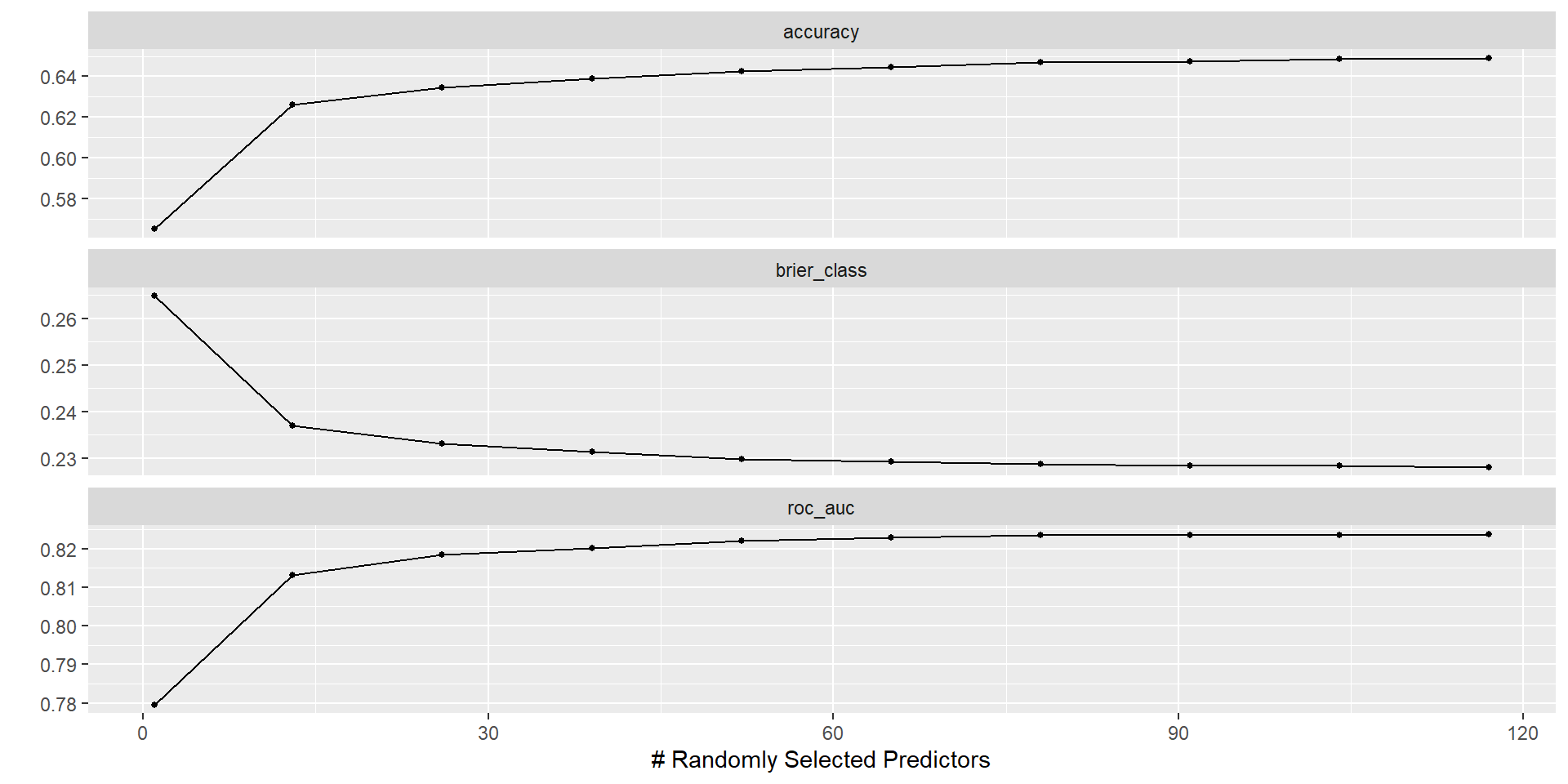
  • Typically \(m = p/3\) for regression and \(m = \sqrt{p}\) for classification but this should be considered a tuning parameter

Define Model

  • trees: kind of a tuning parameter… want to select value that is large enough but doesn’t matter past that
rf_model <- rand_forest(trees = 100, mtry = tune()) |> 
  set_engine("ranger", importance = "impurity") |> 
  set_mode("classification")

Define Recipe

rf_recipe <- recipe(voter_category ~ . , data = voter_train) |> 
  step_indicate_na(all_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_integer(educ, income_cat, Party_ID, Q2_2:Q4_6, Q6, Q8_1:Q9_4, Q14:Q17_4,
               Q25:Q26) |> 
  step_impute_median(all_numeric_predictors()) |> 
  step_impute_mode(all_nominal_predictors()) |> 
  step_dummy(all_nominal_predictors(), one_hot = TRUE)

Define Workflow and Fit

# need to install ranger
rf_wf <- workflow() |> 
  add_model(rf_model) |> 
  add_recipe(rf_recipe)

Upper Limit for mtry

rf_model |> extract_parameter_set_dials()
Collection of 1 parameters for tuning

 identifier type    object
       mtry mtry nparam[?]

Model parameters needing finalization:
   # Randomly Selected Predictors ('mtry')

See `?dials::finalize` or `?dials::update.parameters` for more information.

Extract Number of Features

rf_param <- rf_model |> extract_parameter_set_dials() |> finalize(voter_train)
rf_param
Collection of 1 parameters for tuning

 identifier type    object
       mtry mtry nparam[+]

Tune mtry

voter_folds <- vfold_cv(voter_train, v = 5, repeats = 10, strata = voter_category)

mtry_grid <- grid_regular(rf_param, levels = 10)

tuning_results <- tune_grid(
  rf_wf,
  resamples= voter_folds,
  grid = mtry_grid
)

Results

autoplot(tuning_results)

Evaluate performance

rf_fit <-  rf_wf |> 
  finalize_workflow(select_best(tuning_results)) |> 
  fit(voter_train)

augment(rf_fit, new_data = voter_test) |> 
  accuracy(truth = voter_category, estimate = .pred_class)
# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy multiclass     0.658

Variable Importance

library(vip)
vip(rf_fit)

🔗 MAT 427 - Spring 2025 - Schedule