MATH 427: Boosting

Eric Friedlander

Computational Set-Up

library(tidyverse)
library(tidymodels)
library(rpart.plot)
library(knitr)
library(kableExtra)

tidymodels_prefer()

set.seed(427)

Exploring Bagging Using App

Ensemble Methods

  • Single regression or classification trees usually have poor predictive performance.
  • Ensemble Methods: use a collection of models (in this case, decision trees) to improve the predictive performance
    • Downside: Interpretability
  • Last Time:
    • Bagging
    • Random Forests
  • This Time:
    • Boosting

Flexibility vs. Interpretability

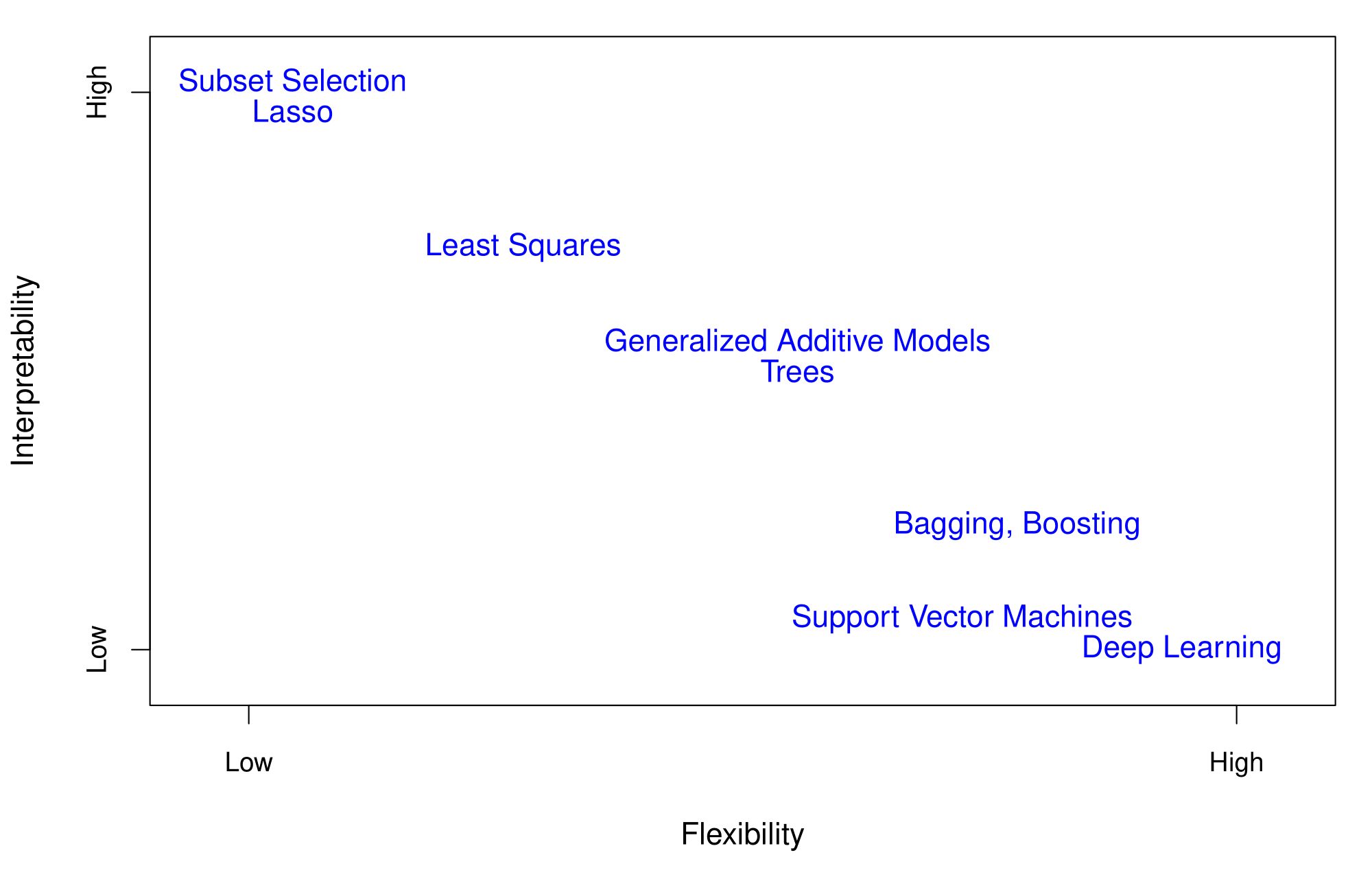
Adapted from ISLR, James et al.

Boosting

Boosting

  • Still an ensemble method in that it creates a bunch of models (trees in this case)
  • Trees are created sequentially, and fit to the residuals of the previous trees
  • Idea: each additional tree to improve upon the previous trees by focusing on places where the previous trees perform poorly
  • Each model in the process is a weak model, referred to as a base learner
  • learning slowly: as more trees are fit, the overall ensemble gradually improves
  • Remind me: What is a residual?

Boosting Algorithm

Let \(B\) be the number of trees you want to fit and \(d\) the maximum number of splits

  1. Set \(\hat{f}(x) = 0\) and \(r_i = y_i\) for all training set
  2. For \(b = 1,\ldots, B\):
    1. Fit tree \(\hat{f}_b\) with \(d\) splits (\(d+1\) leaves) using psuedo-residuals \(r\) as response and features \(X\) as predictors.
    2. Update full model \(\hat{f}\): \(\hat{f} = \hat{f} + \lambda\hat{f}_b\)
    3. Update pseudo-residuals: \(r_i = r_i - \lambda\hat{f}_b(x_i)\)
  3. Output final model: \[\hat{f}(x) = \displaystyle \sum_{b=1}^{B} \lambda \ \hat{f}_b(x)\]
  • It may be hard to see, but this is similar to gradient descent and so is called gradient boosting

Gradient Boosting

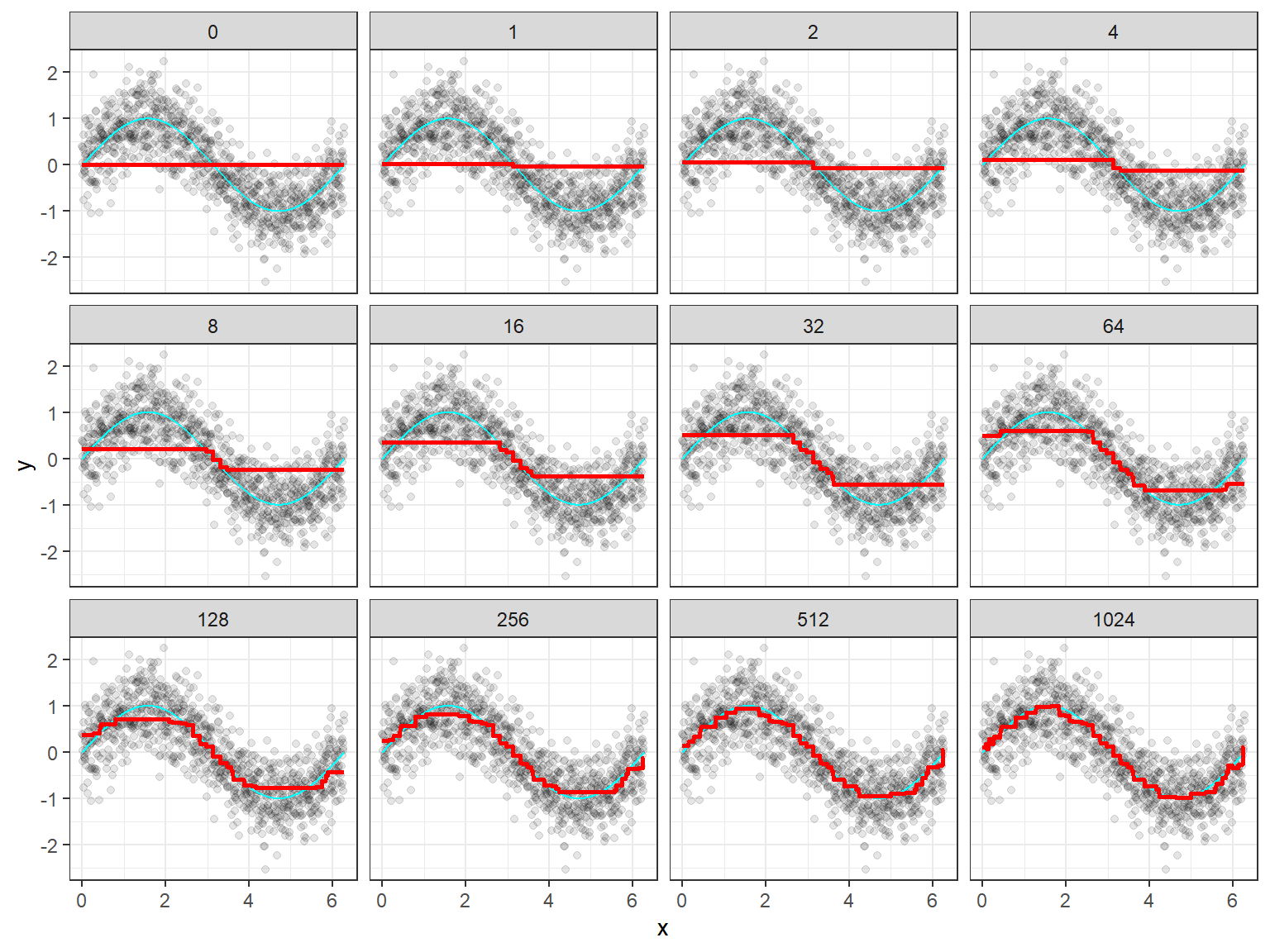
Many Implementations of Boosting

  • Any implementation of boosting you use will like be a tweak of this
    • AdaBoost
    • Catboost
    • LightGBM
    • XGBoost

Gradient Boosting Tuning Parameters

Gradient Boosting in R

Data: Voter Frequency

  • Info about data
  • Goal: Identify individuals who are unlikely to vote to help organization target “get out the vote” effort.
voter_data <- read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/non-voters/nonvoters_data.csv')

voter_clean <- voter_data |> 
  select(-RespId, -weight, -Q1) |>
  mutate(
    educ = factor(educ, levels = c("High school or less", "Some college", "College")),
    income_cat = factor(income_cat, levels = c("Less than $40k", "$40-75k ",
                                               "$75-125k", "$125k or more")),
    voter_category = factor(voter_category, levels = c("rarely/never", "sporadic", "always"))
  ) |> 
  filter(Q22 != 5 | is.na(Q22)) |> 
  mutate(Q22 = as_factor(Q22),
         Q22 = if_else(is.na(Q22), "Not Asked", Q22),
         across(Q28_1:Q28_8, ~if_else(.x == -1, 0, .x)),
         across(Q28_1:Q28_8, ~ as_factor(.x)),
         across(Q28_1:Q28_8, ~if_else(is.na(.x) , "Not Asked", .x)),
         across(Q29_1:Q29_10, ~if_else(.x == -1, 0, .x)),
         across(Q29_1:Q29_10, ~ as_factor(.x)),
         across(Q29_1:Q29_8, ~if_else(is.na(.x) , "Not Asked", .x)),
        Party_ID = as_factor(case_when(
          Q31 == 1 ~ "Strong Republican",
          Q31 == 2 ~ "Republican",
          Q32 == 1  ~ "Strong Democrat",
          Q32 == 2 ~ "Democrat",
          Q33 == 1 ~ "Lean Republican",
          Q33 == 2 ~ "Lean Democrat",
          TRUE ~ "Other"
        )),
        Party_ID = factor(Party_ID, levels =c("Strong Republican", "Republican", "Lean Republican",
                                                "Other", "Lean Democrat", "Democrat", "Strong Democrat")),
        across(!ppage, ~as_factor(if_else(.x == -1, NA, .x))))

Split Data

set.seed(427)

voter_splits <- initial_split(voter_clean, prop = 0.7, strata = voter_category)
voter_train <- training(voter_splits)
voter_test <- testing(voter_splits)

Define Model

  • trees: VERY MUCH A TUNING PARAMETER NOW!
gbm_model <- boost_tree(trees = tune(), learn_rate = tune(), tree_depth = tune(),
                        min_n = tune()) |>
  set_engine("xgboost") |> # dont need importance
  set_mode("classification")

Define Recipe

gbm_recipe <- recipe(voter_category ~ . , data = voter_train) |>
  step_indicate_na(all_predictors()) |>
  step_zv(all_predictors()) |>
  step_integer(educ, income_cat, Party_ID, Q2_2:Q4_6, Q6, Q8_1:Q9_4, Q14:Q17_4,
               Q25:Q26) |>
  step_impute_median(all_numeric_predictors()) |>
  step_impute_mode(all_nominal_predictors()) |>
  step_dummy(all_nominal_predictors(), one_hot = TRUE)

Define Workflow and Fit

gbm_wf <- workflow() |>
  add_model(gbm_model) |>
  add_recipe(gbm_recipe)

Creating Hyperparameter Grid

gbm_grid <- grid_latin_hypercube(trees(range = c(20, 200)),
                                  tree_depth(range = c(1, 15)),
                                  learn_rate(range = c(-10,-1)),
                                  min_n(range = c(2, 40)), size = 50)
voter_folds = vfold_cv(voter_train, v = 5, repeats = 10, strata = voter_category)

Tuning Hyperparameters in Parallel

library(doParallel)

cl <- makePSOCKcluster(9)
registerDoParallel(cl)

tuning_results <- tune_grid(
  gbm_wf,
  resamples= voter_folds,
  grid = gbm_grid
)

stopCluster(cl)

Results

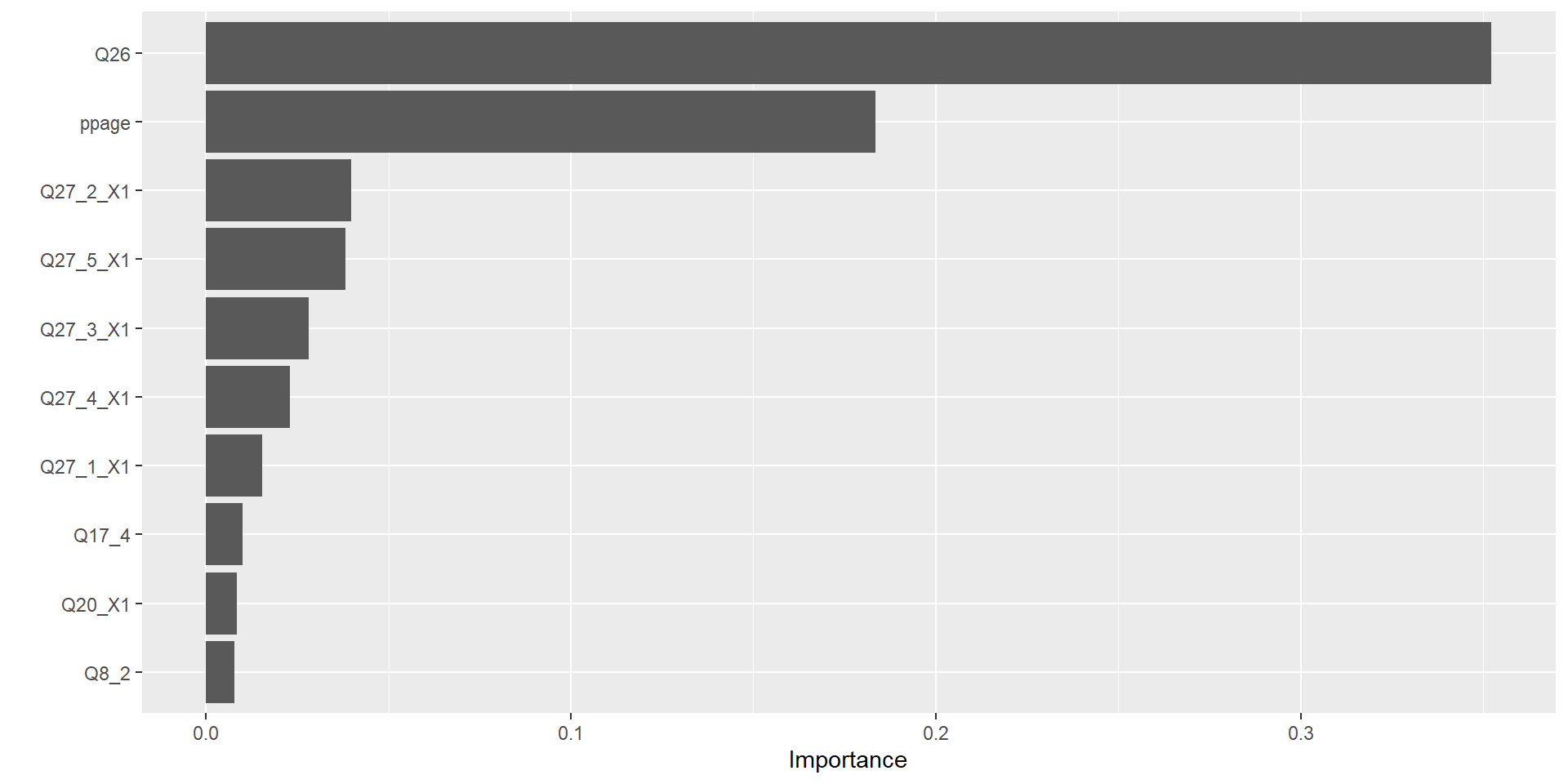
autoplot(tuning_results)

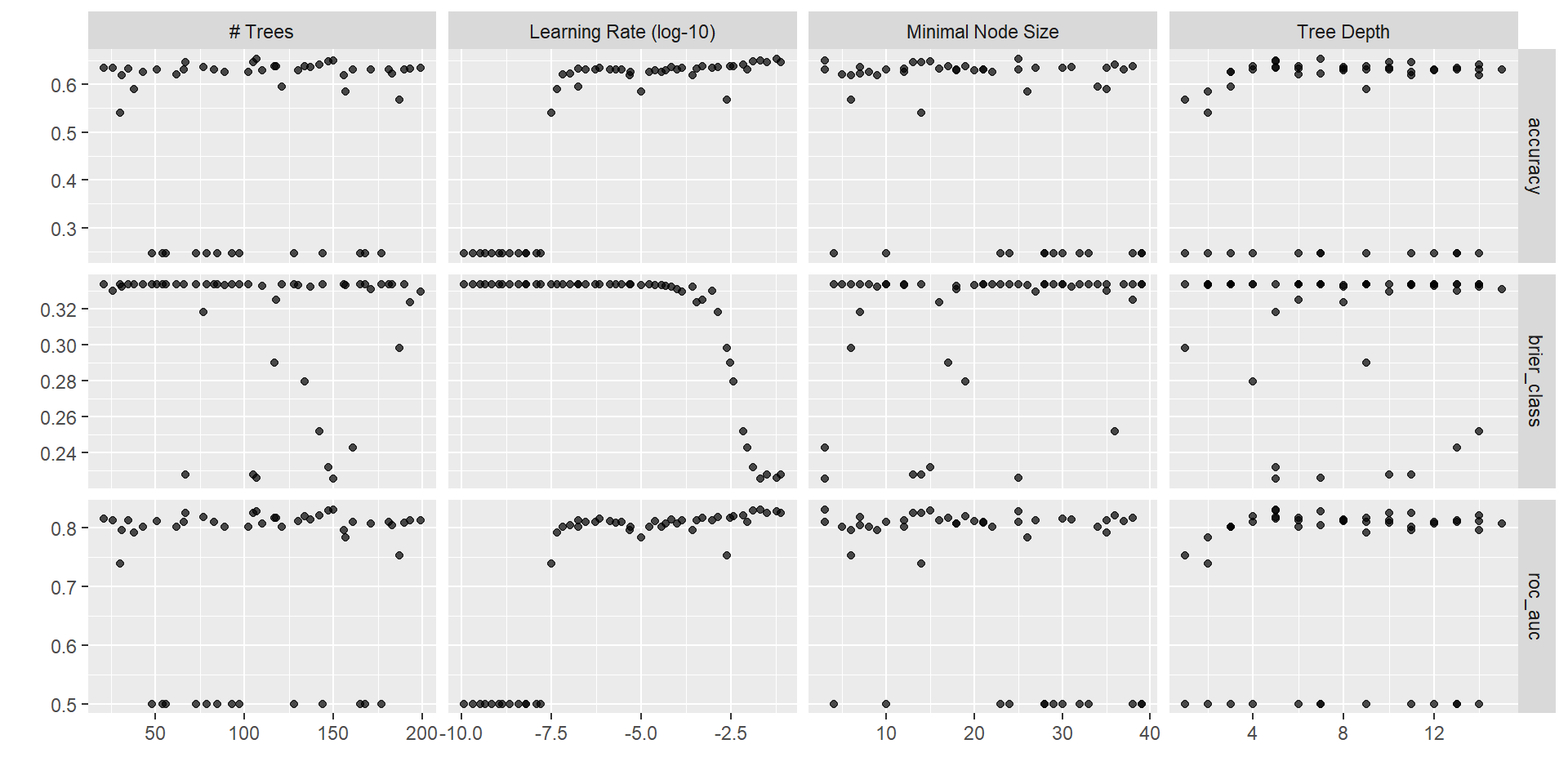
Which one was best?

select_best(tuning_results, metric = "accuracy") |> kable()
trees min_n tree_depth learn_rate .config
107 25 7 0.057429 Preprocessor1_Model24

Evaluate performance

gbm_fit <-  gbm_wf |>
  finalize_workflow(select_best(tuning_results, metric = "accuracy")) |>
  fit(voter_train)

augment(gbm_fit, new_data = voter_test) |>
  accuracy(truth = voter_category, estimate = .pred_class)
# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy multiclass     0.653

Variable Importance

library(vip)
vip(gbm_fit)

🔗 MAT 427 - Spring 2025 - Schedule