MATH 427: More More on Classification

Eric Friedlander

Computational Set-Up

library(tidyverse)
library(tidymodels)
library(knitr)
library(kableExtra)

tidymodels_prefer()

set.seed(427)

Data: Voter Frequency

  • Info about data
  • Goal: Identify individuals who are unlikely to vote to help organization target “get out the vote” effort.
voter_data <- read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/non-voters/nonvoters_data.csv')

voter_clean <- voter_data |>
  select(-RespId, -weight, -Q1) |>
  mutate(
    educ = factor(educ, levels = c("High school or less", "Some college", "College")),
    income_cat = factor(income_cat, levels = c("Less than $40k", "$40-75k ",
                                               "$75-125k", "$125k or more")),
    voter_category = factor(voter_category, levels = c("rarely/never", "sporadic", "always"))
  ) |>
  filter(Q22 != 5 | is.na(Q22)) |>
  mutate(Q22 = as_factor(Q22),
         Q22 = if_else(is.na(Q22), "Not Asked", Q22),
         across(Q28_1:Q28_8, ~if_else(.x == -1, 0, .x)),
         across(Q28_1:Q28_8, ~ as_factor(.x)),
         across(Q28_1:Q28_8, ~if_else(is.na(.x) , "Not Asked", .x)),
         across(Q29_1:Q29_10, ~if_else(.x == -1, 0, .x)),
         across(Q29_1:Q29_10, ~ as_factor(.x)),
         across(Q29_1:Q29_8, ~if_else(is.na(.x) , "Not Asked", .x)),
        Party_ID = as_factor(case_when(
          Q31 == 1 ~ "Strong Republican",
          Q31 == 2 ~ "Republican",
          Q32 == 1  ~ "Strong Democrat",
          Q32 == 2 ~ "Democrat",
          Q33 == 1 ~ "Lean Republican",
          Q33 == 2 ~ "Lean Democrat",
          TRUE ~ "Other"
        )),
        Party_ID = factor(Party_ID, levels =c("Strong Republican", "Republican", "Lean Republican",
                                                "Other", "Lean Democrat", "Democrat", "Strong Democrat")),
        across(!ppage, ~as_factor(if_else(.x == -1, NA, .x))))

Split Data

set.seed(427)

voter_splits <- initial_split(voter_clean, prop = 0.7, strata = voter_category)
voter_train <- training(voter_splits)
voter_test <- testing(voter_splits)

Problem: More than two categories

voter_train |> 
  ggplot(aes(x = voter_category)) +
  geom_bar()

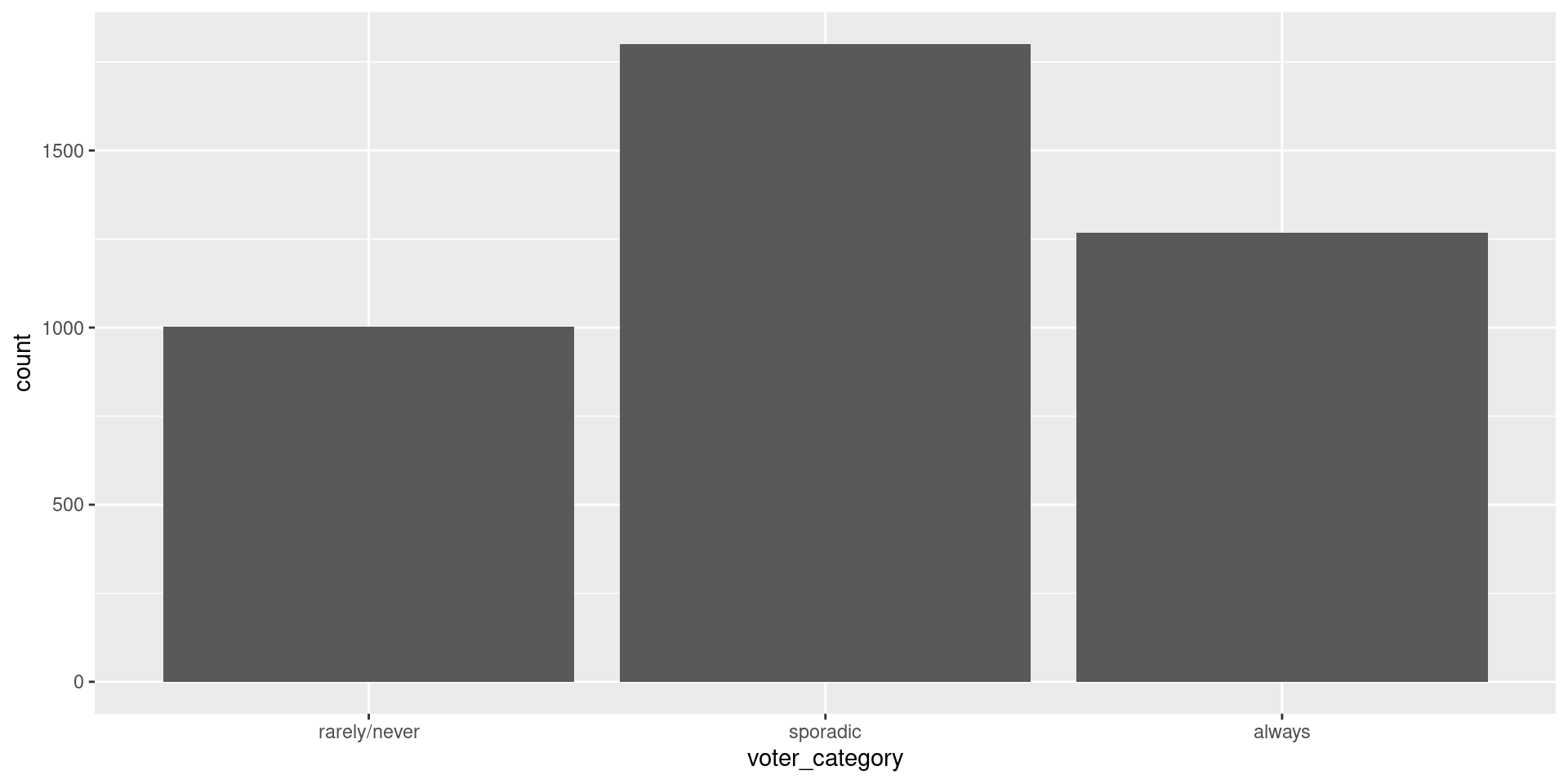
Define Model: Multinomial Regression

mn_reg_model <- multinom_reg(mixture = 1, penalty = 0.005) |> # I chose this penalty arbitrarily
  set_engine("glmnet", family = "multinomial") |> 
  set_mode("classification")

Define Recipe

mr_recipe <- recipe(voter_category ~ . , data = voter_train) |>
  step_zv(all_predictors()) |>
  step_integer(educ, income_cat, Party_ID, Q2_2:Q4_6, Q6, Q8_1:Q9_4, Q14:Q17_4,
               Q25:Q26) |>
  step_impute_median(all_numeric_predictors()) |>
  step_impute_mode(all_nominal_predictors()) |>
  step_dummy(all_nominal_predictors(), one_hot = FALSE) |> 
  step_normalize(all_numeric_predictors())

Define Workflow and Fit

mr_fit <- workflow() |>
  add_model(mn_reg_model) |>
  add_recipe(mr_recipe) |> 
  fit(voter_train)

Look at Predictions

mr_fit |> augment(new_data = voter_test) |> slice_sample(n=10) |> select(1:4) |> head() |>  kable()
.pred_class .pred_rarely/never .pred_sporadic .pred_always
sporadic 0.0317402 0.5122327 0.4560271
always 0.0463060 0.4464935 0.5072005
sporadic 0.0553279 0.6529393 0.2917328
always 0.0388506 0.4351109 0.5260385
always 0.0361359 0.4164662 0.5473979
always 0.0991499 0.4310622 0.4697879

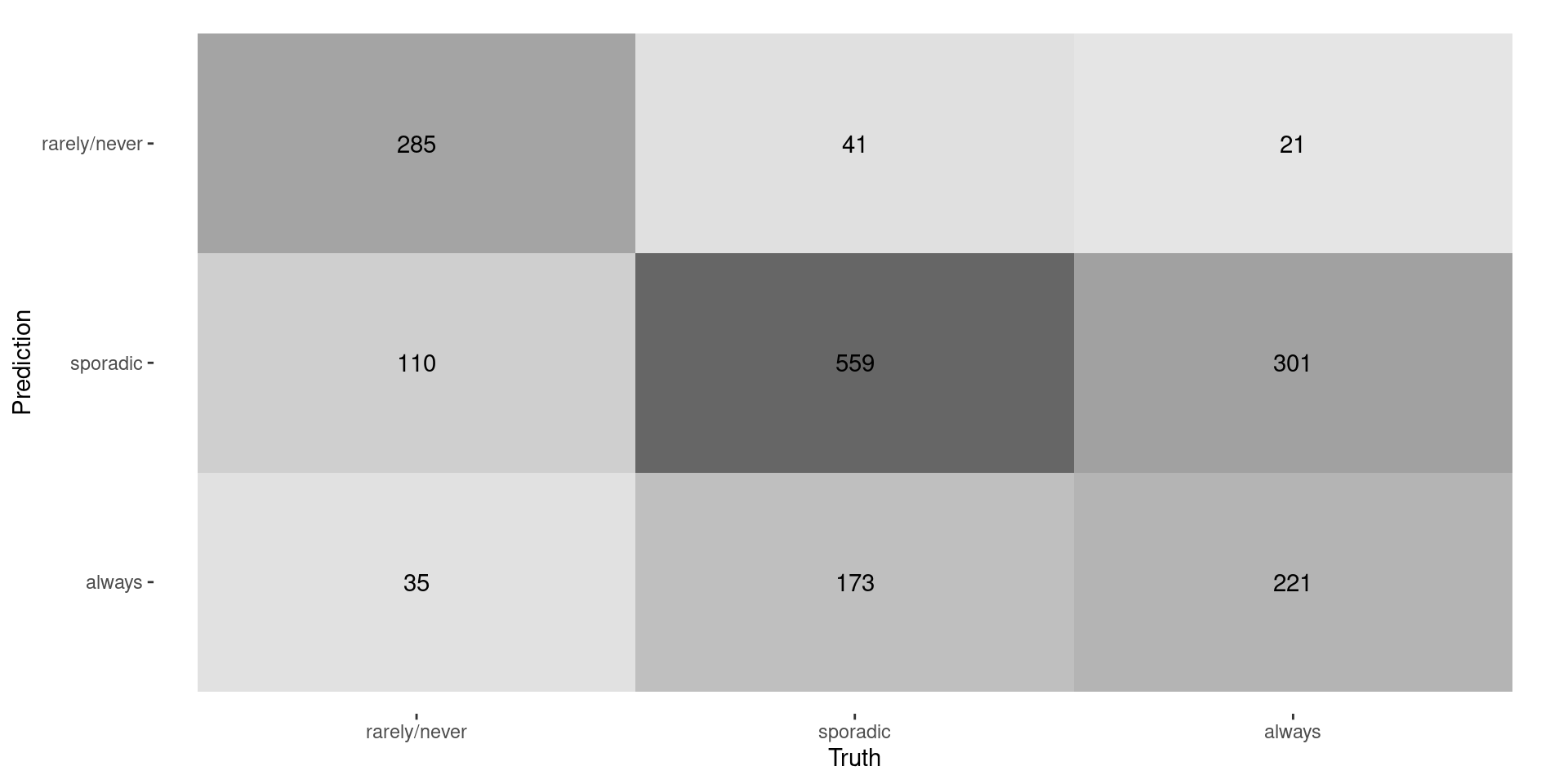
Confusion Matrix

mr_fit |> augment(new_data = voter_test) |> 
  conf_mat(truth = voter_category, estimate = .pred_class) |> autoplot("heatmap")

Last Time

  • No “Positive” and “Negative” anymore
  • Most of our metrics were based on having “Positive” vs. “Negative”
  • Solution 1: 1-vs-all metrics

Evaluating Multiclass Models

  • Solution 2: Average metrics across labels
    • Macro-averaging average one-versus-all metrics
      • Recall: \(\frac{0.66+0.72+0.41}{3} \approx 0.60\)
    • Macro-weighted averaging same but weight by class size
      • Recall: \(\frac{430\times 0.66+773\times 0.72+543\times 0.41}{1746} \approx 0.61\)
    • Micro-averaging compute contribution for each class, aggregates them, then computes a single metric
      • Recall: \(\frac{285+559+221}{430+779+543} \approx 0.61\)

Questions From Last Time

  • Multinomial Logistic regression:
    • Each class \(k\): \[\log \frac{\text{Prob. class } k}{\text{Prob. class } K} = \beta_{0k} + \beta_{1k}X_1 + \cdots + \beta_{pk}X_p\]
  • Shuba: Micro-averaged recall is the same as accuracy… CORRECT!
    • Same is true of precision AND \(F_1\)
    • Useful if you have a “multi-label” classification problem (not covered in this class)

Rabin’s Question

  • “What does a medium sized data set mean?”
  • Idea behind ML: identify patterns in data and use them to make predictions
  • As data gets “bigger”:
    • Patterns become clearer
    • Computational complexity increases
  • Informal definitions:
    • Small data: not enough data to fully represent patterns
    • Big data: all the info is there but special approaches need to be taken to handle all the data

Thinking about small data

  • Patterns not fully represented in data \(\Rightarrow\) restrict the set of possible patterns and give model less flexibility and freedom
    • Logistic regression (probably with regularization)
    • Support vector machines (we haven’t talked about these yet)
    • To a lesser extent: Decision Trees
    • NOT KNN

Thinking about big data

  • Patterns are definitely there but size introduces computational problems
    • Data set can’t fit in memory
      • Solution 1: Use a high-memory HPC cluster node
      • Solution 2: Modify algorithms to use parts of data instead of full data set (e.g. Stochastic gradient descent)
    • Algorithm scales with size of data and will take too long to run/fit
      • Solution 1: Run in parallel if possible using HPC cluster
      • Solution 2: Develop faster algorithms
        • Implement in a compiled language like C
        • Develop (faster) approximate solution
  • Curse of dimensionalality
    • If \(p\) is too-big \(\Rightarrow\) too much space and things are too far apart \(\Rightarrow\) similar impact to small data but without computational benefit
  • Note: big \(n\) vs. big \(p\) can present different issues

Medium Data

  • Data that’s big enough to have (most) of the information you need but not so big that it presents computational issues
  • KNN sweet spot
    • Enough data the “nearest-neighbors” are actually “near”
    • Not so much data that it takes forever to make predictions

Exploring with App

Macro-Averaging in R

voter_metrics <- metric_set(accuracy, precision, recall)

mr_fit |> augment(new_data = voter_test) |> 
  voter_metrics(truth = voter_category, estimate = .pred_class, estimator = "macro") |> 
  kable()
.metric .estimator .estimate
accuracy multiclass 0.6099656
precision macro 0.6375886
recall macro 0.5976485

Macro-Weighted Averaging in R

mr_fit |> augment(new_data = voter_test) |> 
  voter_metrics(truth = voter_category, estimate = .pred_class, estimator = "macro_weighted") |> 
  kable()
.metric .estimator .estimate
accuracy multiclass 0.6099656
precision macro_weighted 0.6176222
recall macro_weighted 0.6099656

Micro-Averaging in R

mr_fit |> augment(new_data = voter_test) |> 
  voter_metrics(truth = voter_category, estimate = .pred_class, estimator = "micro") |> 
  kable()
.metric .estimator .estimate
accuracy multiclass 0.6099656
precision micro 0.6099656
recall micro 0.6099656

What if output is probability?

  • For binary case we used ROC curve and AUC…
  • Similar ideas apply here:
    • One vs. all
    • Macro Averaging
    • NO MICRO AVERAGING!
    • Hand and Till extension of AUC

Plotting one-vs.-all

mr_fit |> augment(new_data = voter_test) |> 
  roc_curve(truth = voter_category, `.pred_rarely/never`, .pred_sporadic, .pred_always) |> 
  autoplot()

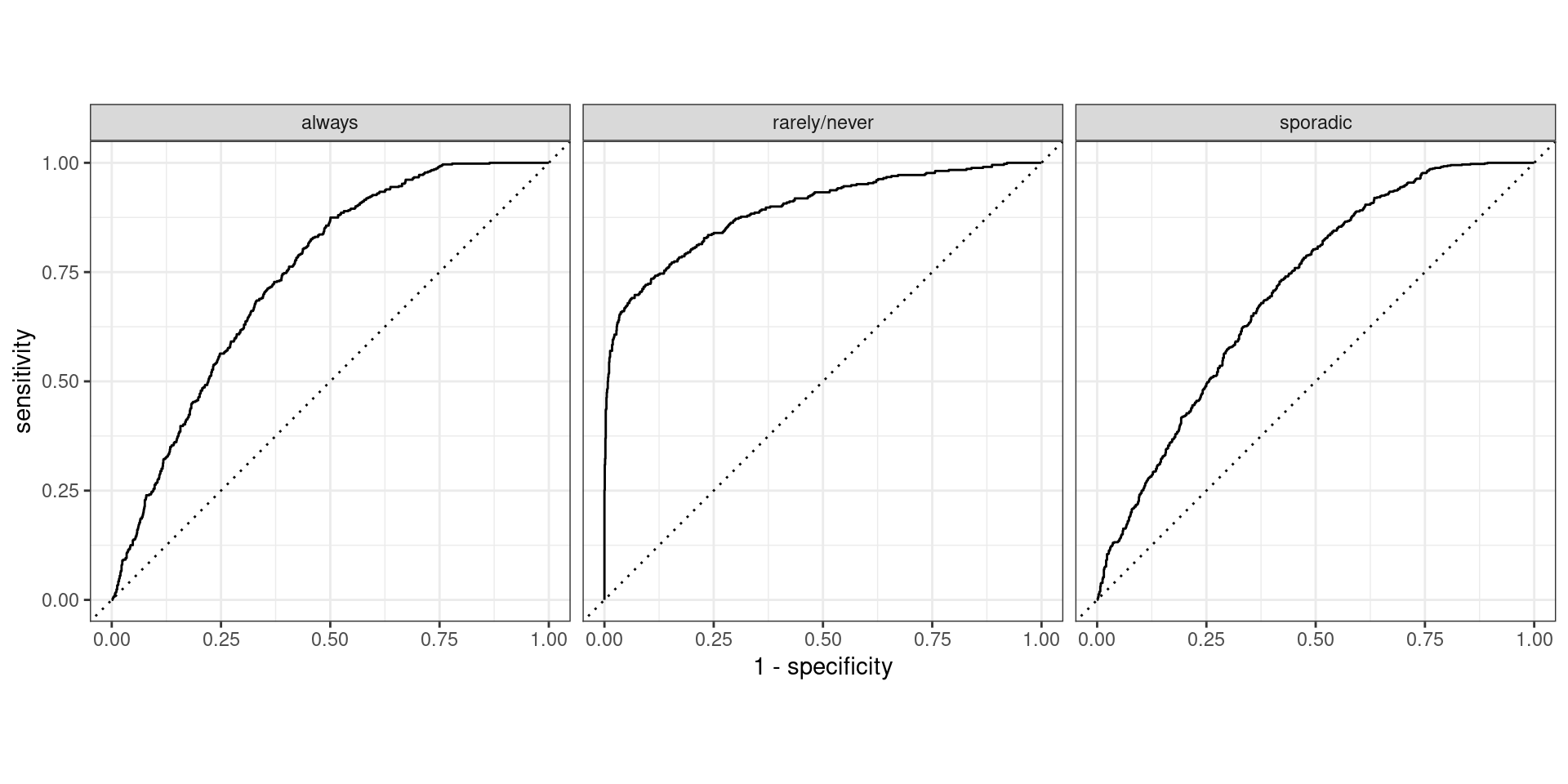
Macro Averaged AUC

mr_fit |> augment(new_data = voter_test) |> 
  roc_auc(truth = voter_category, `.pred_rarely/never`, .pred_sporadic, .pred_always, 
          estimator = "macro") |> 
  kable()
.metric .estimator .estimate
roc_auc macro 0.7802495

Macro-Weighted Averaged AUC

mr_fit |> augment(new_data = voter_test) |> 
  roc_auc(truth = voter_category, `.pred_rarely/never`, .pred_sporadic, .pred_always, 
          estimator = "macro_weighted") |> 
  kable()
.metric .estimator .estimate
roc_auc macro_weighted 0.7636223

Hand and Till AUC

  • Idea behind traditional AUC: “How well are my classes being separated?”
  • Hand and Till: Extend this idea to multiple-classes
  • Paper
    • Basic Idea: Do pairwise comparison of classes and average
mr_fit |> augment(new_data = voter_test) |> 
  roc_auc(truth = voter_category, `.pred_rarely/never`, .pred_sporadic, .pred_always) |> 
  kable()
.metric .estimator .estimate
roc_auc hand_till 0.7967478

Discussion

  • Why do you compute averages/means?
  • How would heavily imbalanced classes impact each type of averaging?
    • Which type(s) of averaging weight(s) each class equally regardless of balance?
    • Which type(s) of averaging favor(s) larger classes?
    • Does this imply that one is better than the others?

Exploring with App

  • App
    • Break into groups
    • Investigate how your performance metrics change between balanced data and unbalanced data
    • Additional Considerations:
      • Impact of boundaries/models?
      • Impact of sample size?
      • Impact of noise level?
    • Please write down observations so we can discuss

🔗 MAT 427 - Spring 2025 - Schedule