MATH 427: Class Imbalance
Eric Friedlander
Computational Set-Up
Exploring with App
- App
- Break into groups
- Investigate how your performance metrics change between balanced data and unbalanced data
- Additional Considerations:
- Impact of boundaries/models?
- Impact of sample size?
- Impact of noise level?
- Please write down observations so we can discuss
Dealing with Class-Imbalance
Class-Imbalance
- Class-imbalance occurs where your the classes in your response greatly differ in terms of how common they are
- Occurs frequently:
- Medicine: survival/death
- Admissions: enrollment/non-enrollment
- Finance: repaid loan/defaulted
- Tech: Clicked on ad/Didn’t click
- Tech: Churn rate
- Finance: Fraud
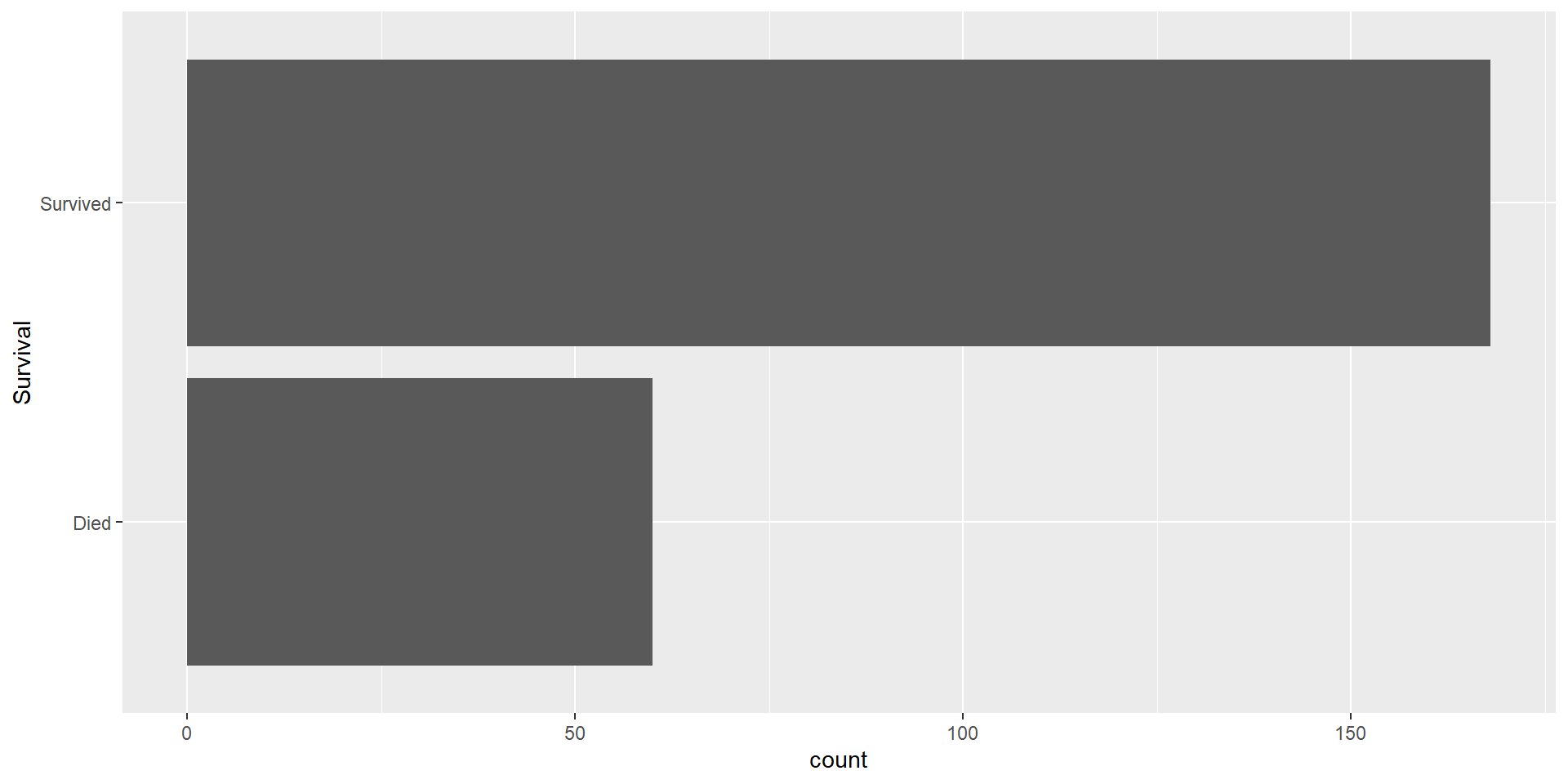
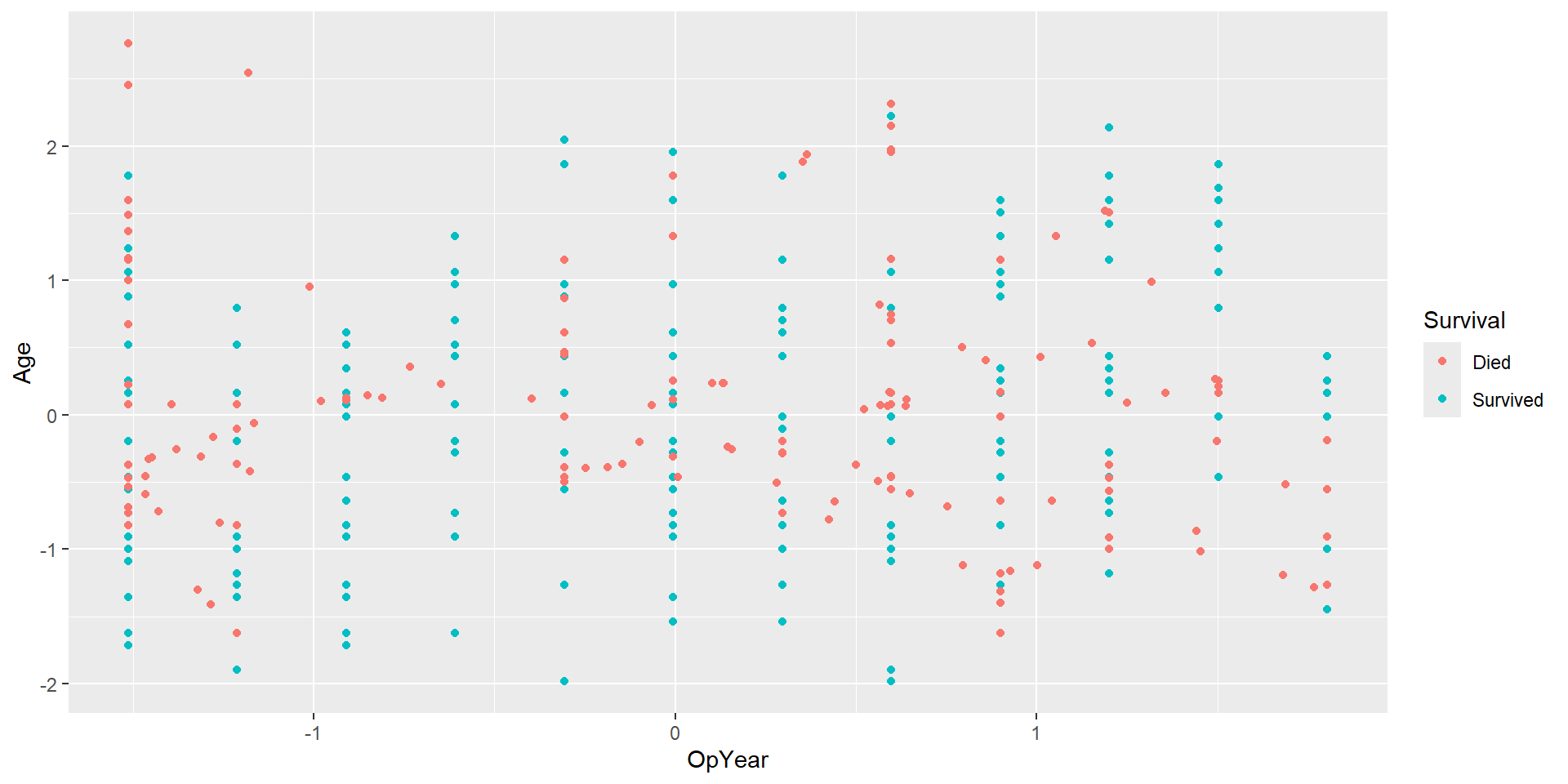
Data: haberman
Study conducted between 1958 and 1970 at the University of Chicago’s Billings Hospital on the survival of patients who had undergone surgery for breast cancer.
Goal: predict whether a patient survived after undergoing surgery for breast cancer.
Quick Clean
Split Data
Visualizing Response
Fitting Model
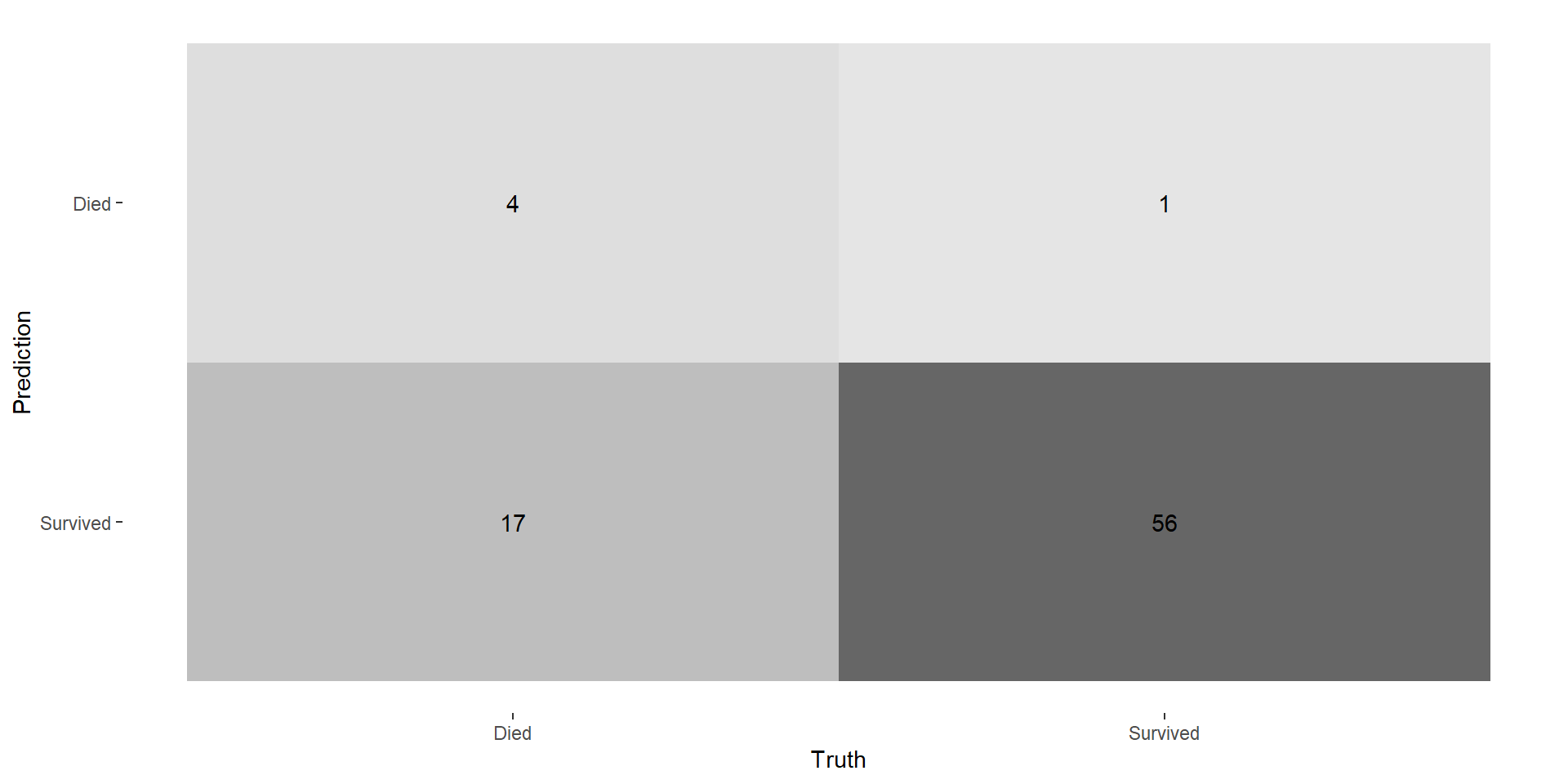
Confusion Matrix
Performance Metrics
hab_metrics <- metric_set(accuracy, precision, recall)
lr_fit |> augment(new_data = hab_test) |>
roc_auc(truth = Survival, .pred_Died) |> kable()| .metric | .estimator | .estimate |
|---|---|---|
| roc_auc | binary | 0.7284879 |
lr_fit |> augment(new_data = hab_test) |>
hab_metrics(truth = Survival, estimate = .pred_class) |> kable()| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | binary | 0.7692308 |
| precision | binary | 0.8000000 |
| recall | binary | 0.1904762 |
Recall is BAD!
- Since there are so few deaths, model always predicts a low probability of death
- Idea: just because you you have a HIGHER probability of death doesn’t mean have a HIGH probability of death
What do we do?
- Depends on what your goal is…
- Ask yourself: What is most important to my problem?
- Accurate probabilities?
- Overall accuracy?
- Effective identification of a specific class (e.g. positives)?
- Low false-positive rate?
- Discussion: Let’s think of scenarios where each one of these is the most important.
Solutions to Class Imbalance
- Adjust probability threshold (we’ve already done this)
- If you wanted to increase your recall would you increase or decrease your threshold?
- Sampling-based solutions (done during pre-processing)
- Over-sample minority class
- Under-sample majority class
- Combination of both (e.g. SMOTE)
- Weight class/objective function
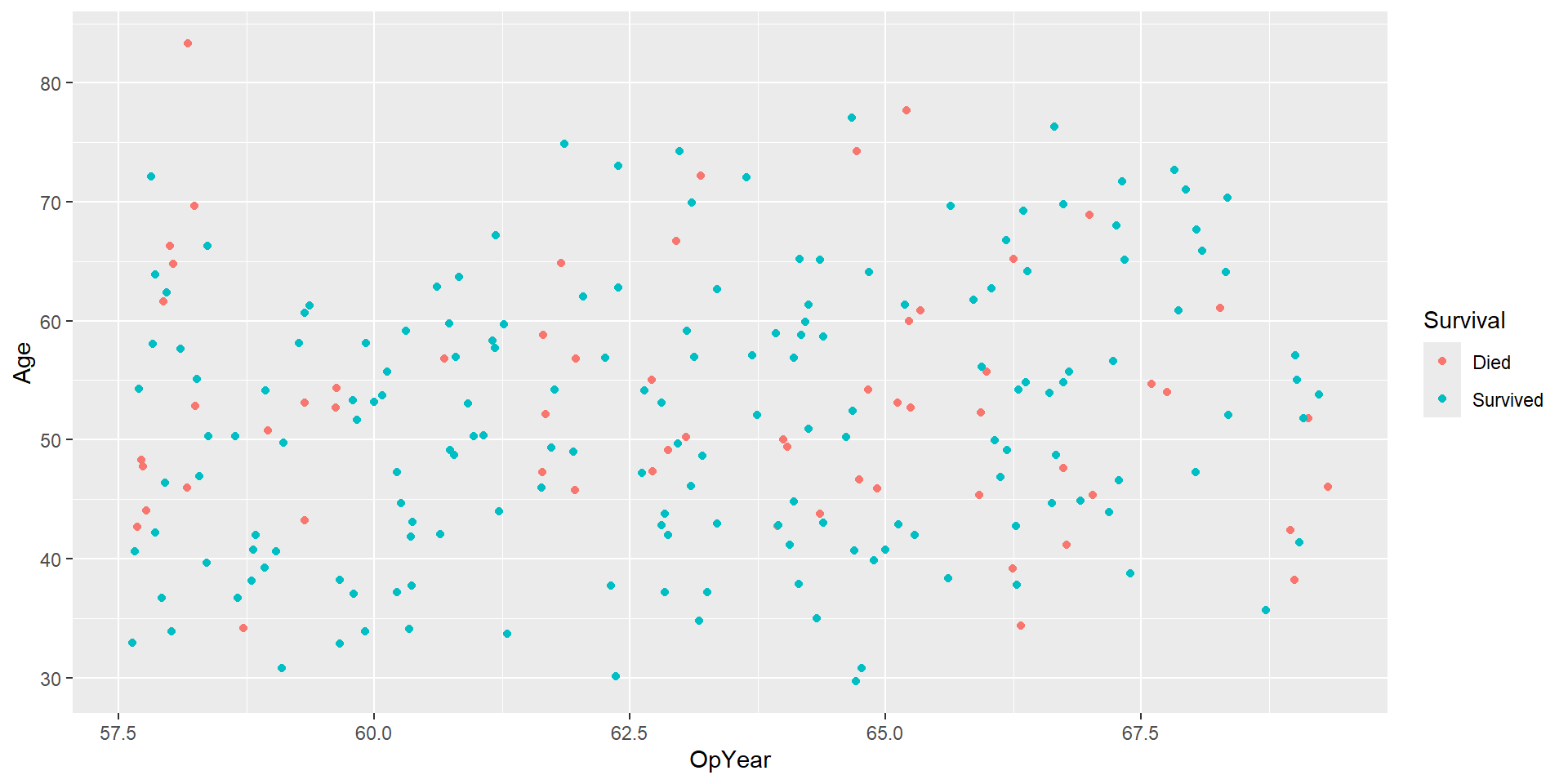
Over-sampling minority class
- Upsample: think bootstrapping for final sample is larger than original
- Idea: upsample minority class until it is same size(ish) as majority class
Visualizing Data
Upsample Recipe
Upsampled Data
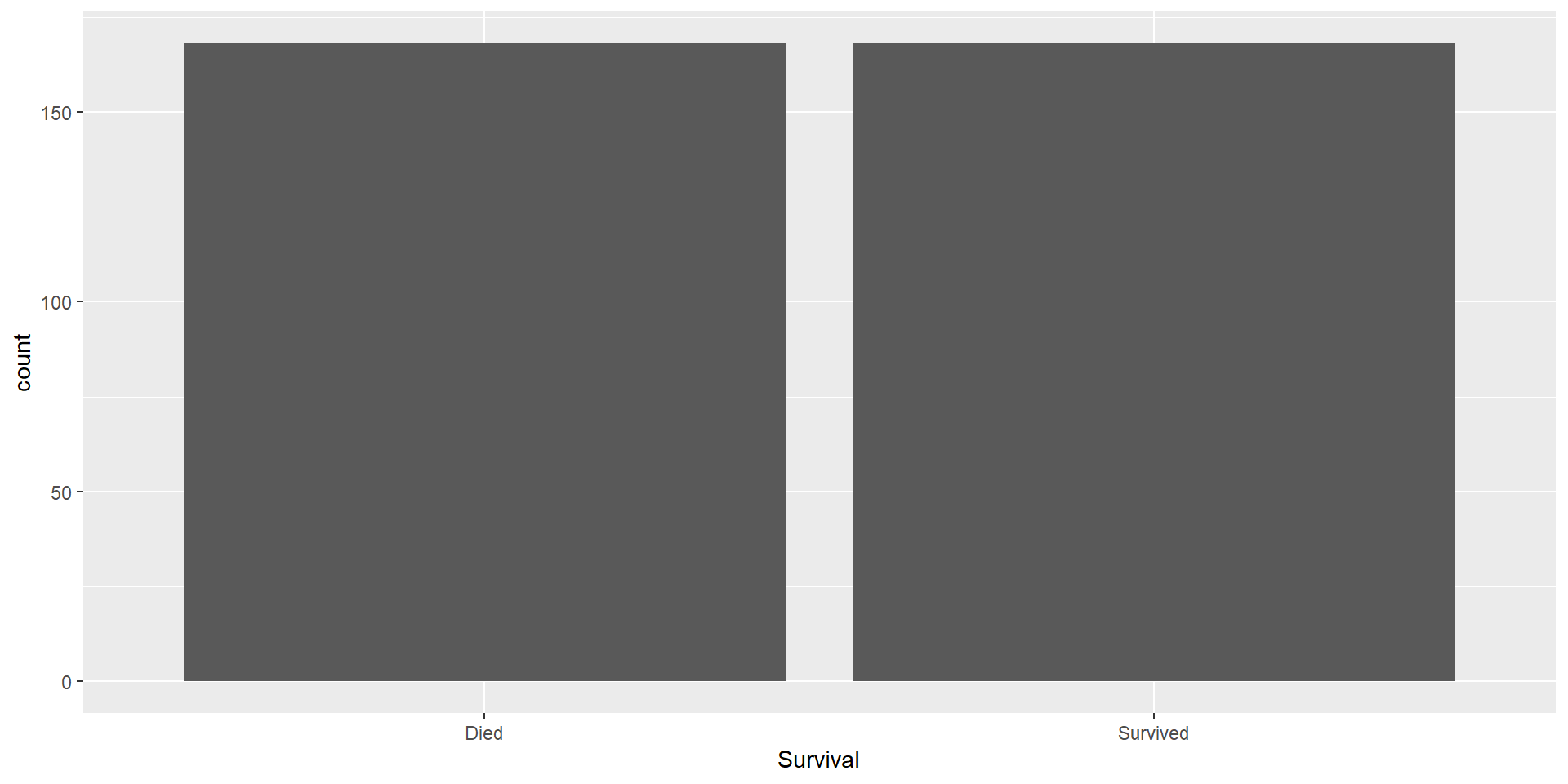
Visualizing Upsampled Data
Visualizing Upsampled Data: No Jitter
Performance consideration
- Pro:
- Preserves all information in the data set
- Con:
- Models will probably over-align to the noise in the minority class
Under-sampling majority class
- Downsample: collect a random sample smaller than the original sample
- Idea: down sample majority class until it is same size(ish) as minority class
Visualizing Data
Downsample Recipe
Downsample Data

Visualizing Downsampled Data
Visualizing Downsampled Data: No Jitter
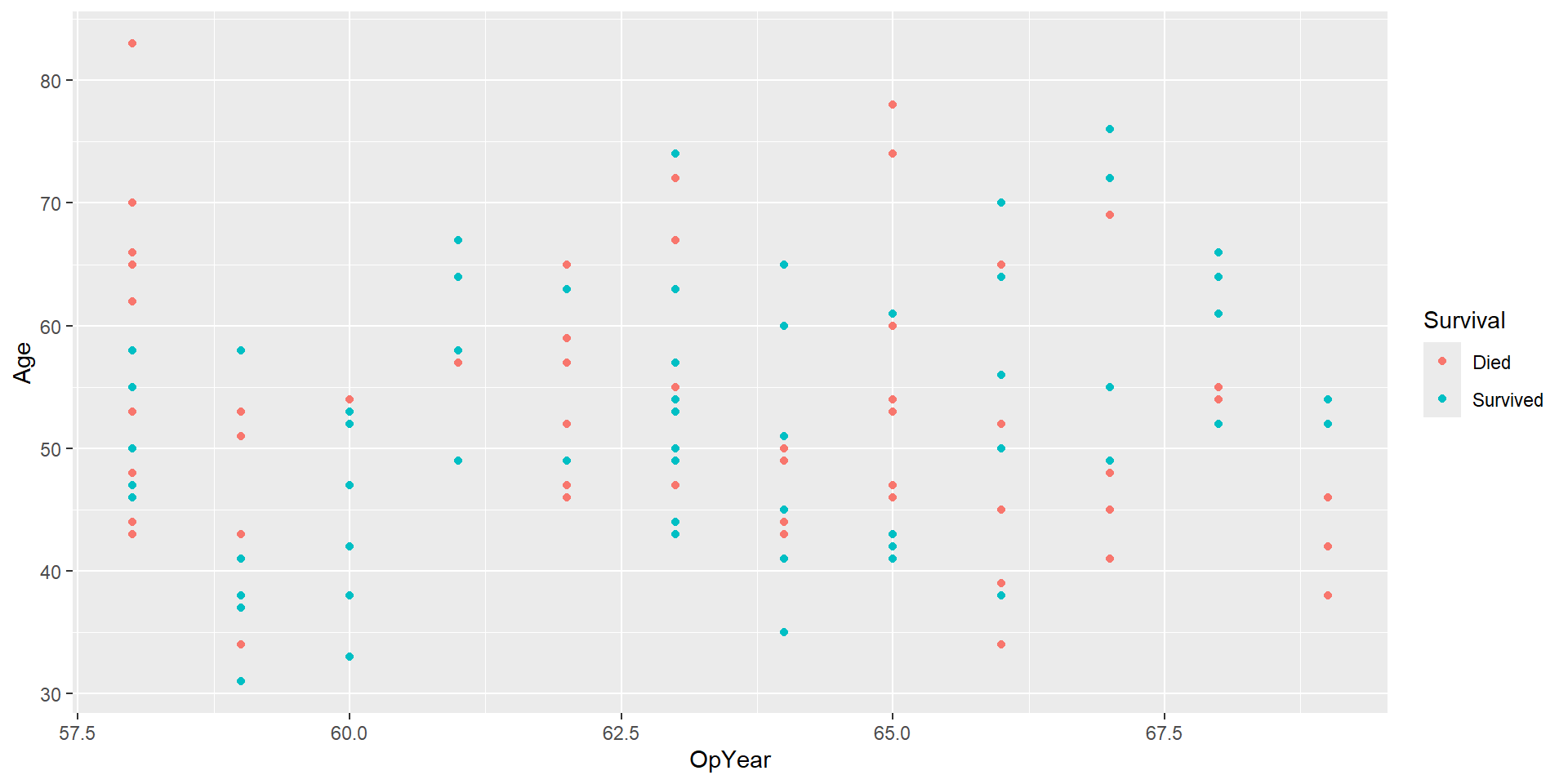
Performance considerations
- Pro:
- Model doesn’t over-align to noise in minority class
- Con:
- Lose information from majority class
SMOTE
- Basic idea:
- Both upsample minority and downsample majority (Tidymodel implementation only upsamples)
- Better Upsampling: Instead of just randomly replicating minority observations
- Find (minority) nearest neighbors of each minority observation
- Interpolate line between them
- Upsample by randomly generating points in interpolated lines
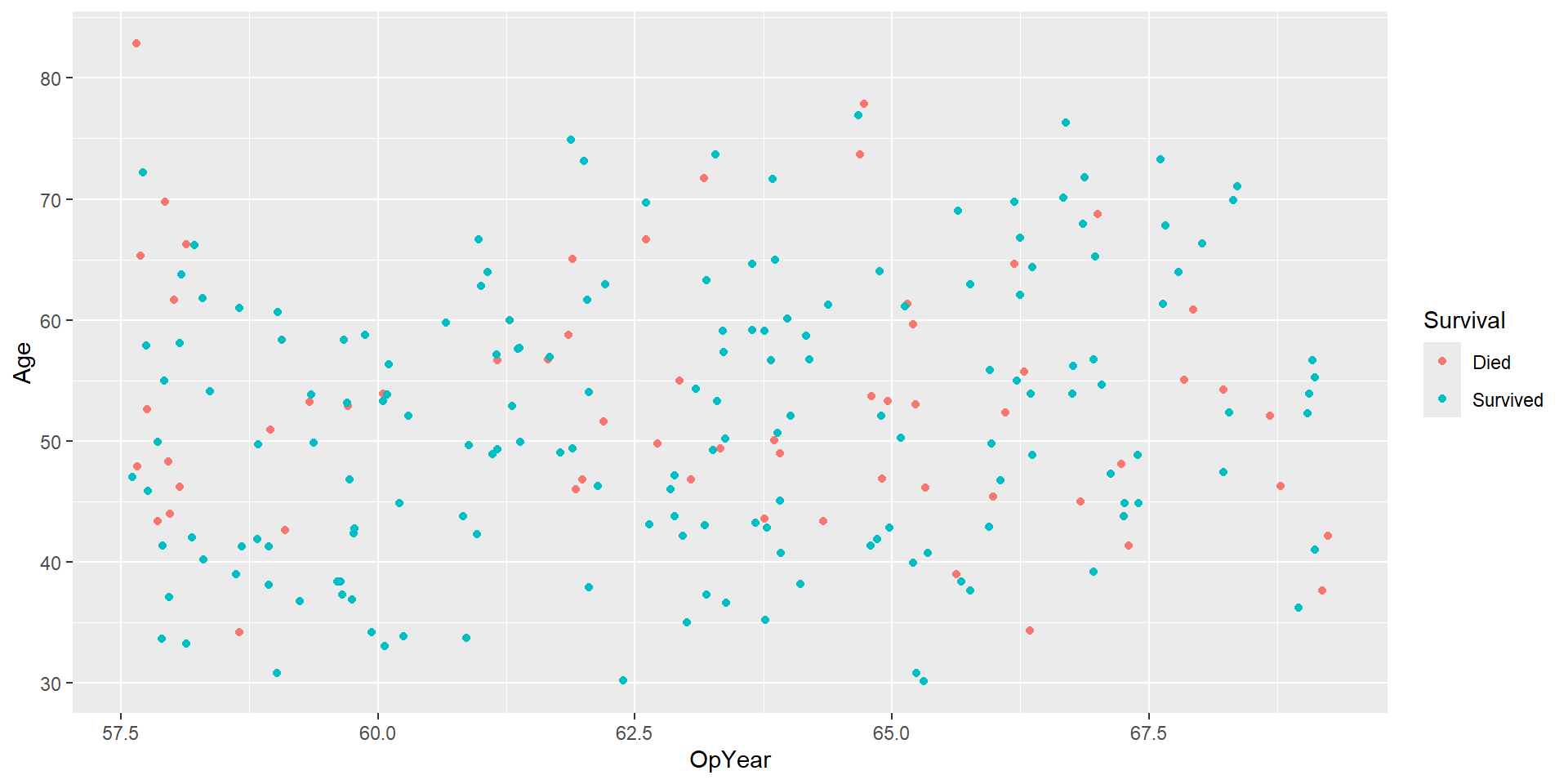
Visualizing Data
SMOTE Recipe
SMOTE Data
Visualizing SMOTE Data
Visualizing SMOTE Data: No Jitter
Performance considerations
- Pro:
- Model doesn’t over-align (as much) to noise in minority class
- Don’t lose (as much) information from majority class
- Con:
- Creating new information out of nowhere
Fitting models
Evaluate Performance
| .metric | .estimator | .estimate |
|---|---|---|
| roc_auc | binary | 0.7343358 |
| .metric | .estimator | .estimate |
|---|---|---|
| roc_auc | binary | 0.7243108 |
| .metric | .estimator | .estimate |
|---|---|---|
| roc_auc | binary | 0.7251462 |
Evaluate Performance
| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | binary | 0.7692308 |
| precision | binary | 0.5714286 |
| recall | binary | 0.5714286 |
| .metric | .estimator | .estimate |
|---|---|---|
| accuracy | binary | 0.7435897 |
| precision | binary | 0.5217391 |
| recall | binary | 0.5714286 |
Weighting Observations/Objective Function
Creating Importance Weights
Weighted Workflow
Model Performance
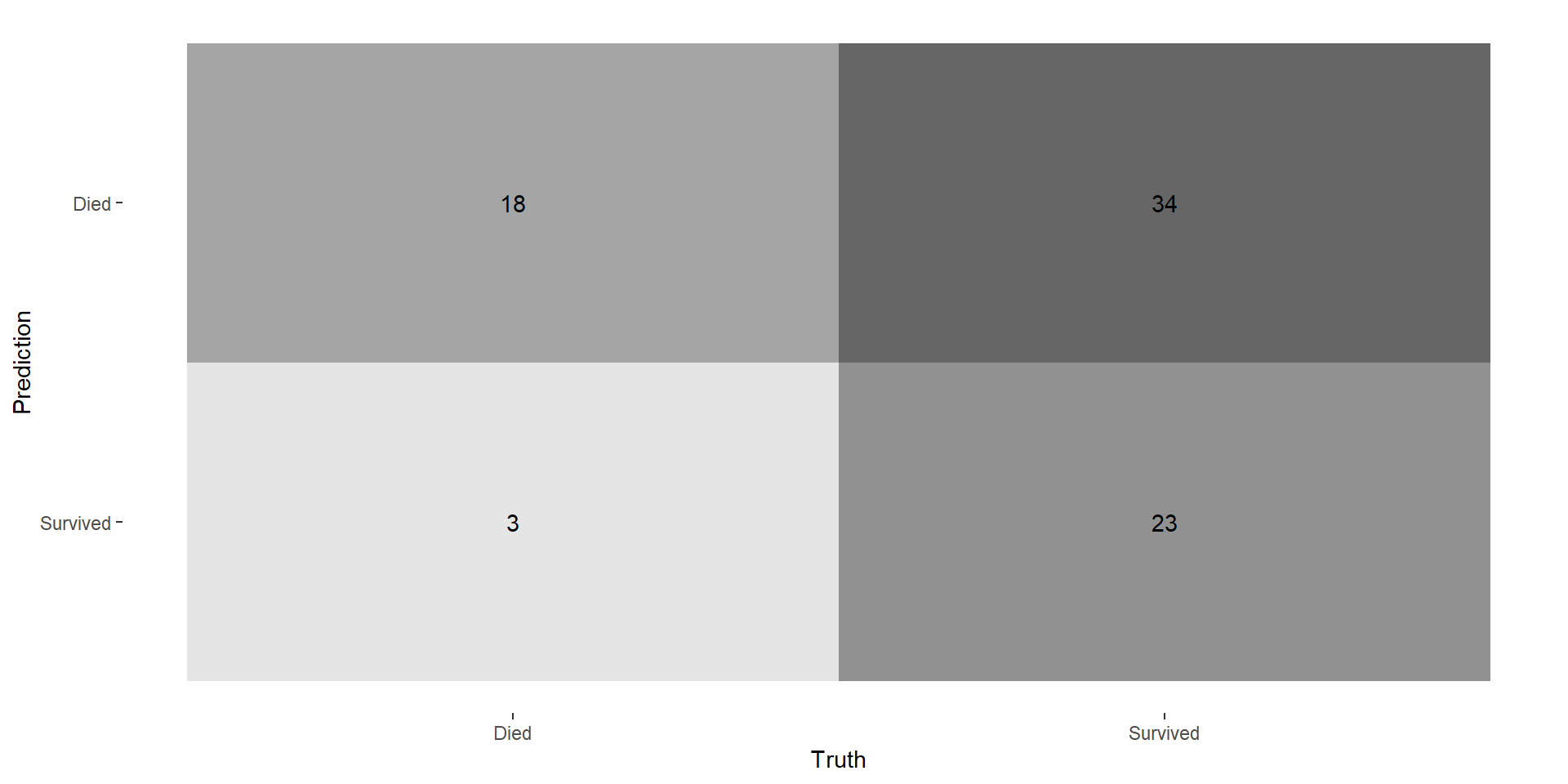
Model Performance
Final Note / Alternative Metrics
Model vs Decisions
- Helpful framework for thinking about this:
- Divide model predictions from decisions
- Usually, model predicts a probability, then you make a classification based on that probability
- Choosing the best model probably means (1) calibrating your probabilities correctly, then (2) making classifications/decisions to optimze your use-case
Scoring Rules
- Scoring rule: metric that evaluates probabilities
- Notation:
- \(\hat{p}_{ik}\): predicted probability observation \(i\) is in class \(k\)
- \(y_{ik}\): 1 if observation \(i\) is in class \(k\), 0 otherwise
- \(K\): number of classes
- \(N\): number of observations
- Brier Score: think MSE for probabilities
- Binary: \(\frac{1}{N} \sum_{i=1}^{N} (\hat{p}_i - y_i)^2\)
- Multiclass: \(\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} (\hat{p}_{ik} - y_{ik})^2\)
- Logorithmic Score:
- Binary: \(-\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{p}_i) + (1 - y_i) \log(1 - \hat{p}_i) \right]\)
- Multi-class: \(-\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} y_{ik} \log(\hat{p}_{ik})\)
Scoring our models
hab_scores <- metric_set(brier_class, mn_log_loss, roc_auc)
all_scores <- lr_fit |> augment(new_data = hab_test) |> hab_scores(truth = Survival, .pred_Died) |> mutate(model = "Logistic") |>
bind_rows(oversamp_fit |> augment(new_data = hab_test) |> hab_scores(truth = Survival, .pred_Died) |> mutate(model = "Oversample")) |>
bind_rows(downsamp_fit |> augment(new_data = hab_test) |> hab_scores(truth = Survival, .pred_Died) |> mutate(model = "Undersample")) |>
bind_rows(smote_fit |> augment(new_data = hab_test) |> hab_scores(truth = Survival, .pred_Died) |> mutate(model = "SMOTE")) |>
bind_rows(weighted_fit |> augment(new_data = hab_test) |> hab_scores(truth = Survival, .pred_Died) |> mutate(model = "Weighted"))Scores
all_scores |>
select(-.estimator) |>
pivot_wider(names_from = .metric, values_from = .estimate) |>
kable()| model | brier_class | mn_log_loss | roc_auc |
|---|---|---|---|
| Logistic | 0.1678374 | 0.5161121 | 0.7284879 |
| Oversample | 0.2115716 | 0.6217420 | 0.7343358 |
| Undersample | 0.2130135 | 0.6298389 | 0.7243108 |
| SMOTE | 0.2169736 | 0.6304324 | 0.7251462 |
| Weighted | 0.2599917 | 0.7217460 | 0.7142857 |
Conclusion
- Many different approaches and strategies depending on data
- First strategy: tresholding
- Many times method depends on model algorithm
- Make sure to ask “Is imbalance really a problem here?”
